Duas partículas têm massas iguais a e cargas iguais a . Devido a sua interação eletrostática, elas sofrem uma força quando estão separadas de uma distância . Em seguida, estas partículas são penduradas, a partir de um mesmo ponto, por fios de comprimento e ficam equilibradas quando a distância entre elas é . A cotangente do ângulo que cada fio forma com a vertical, em função de , , , , e , é
Segundo enunciado, podemos esboçar as duas situações como:
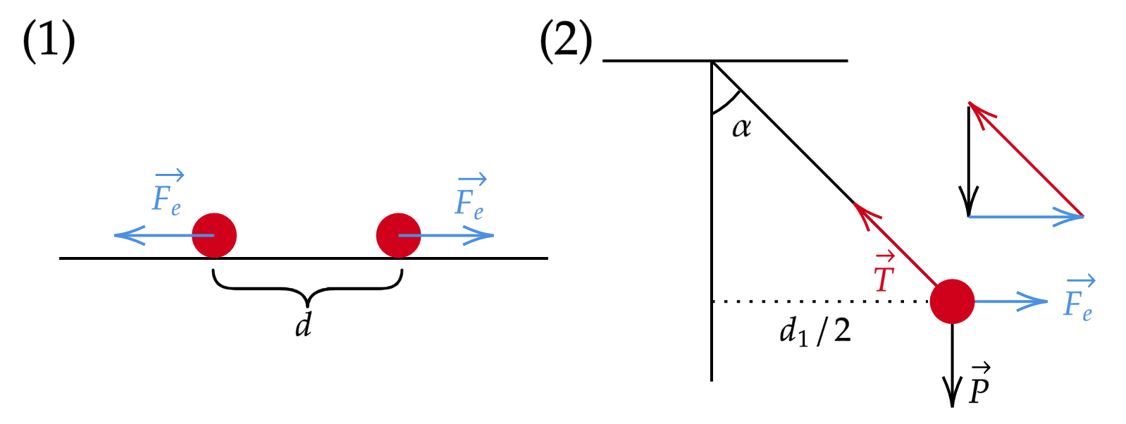Na primeira situação, analisando uma das cargas, temos:
\begin{matrix} F = F_e &\Rightarrow& Fd^2 = KQ^2
\end{matrix}Já na segunda situação, decompondo a tração encontramos duas equações, das quais constatamos:
\begin{matrix} T\cos{\alpha} = mg &&,&& T\sin{\alpha} = {\dfrac{KQ^2}{(d_1)^2}}
\end{matrix} Continuando, \begin{matrix} \cot{\alpha} = {\dfrac{mg(d_1)^2}{KQ^2}} &\Rightarrow& \fbox{$\cot{\alpha} = {\dfrac{mg(d_1)^2}{(Fd^2)}}$}
\end{matrix} \begin{matrix} Letra \ (C)
\end{matrix}
Ampliar Imagem
