Considere as seguintes afirmações :
I - Se um espelho plano transladar de uma distância ao longo da direção perpendicular a seu plano, a imagem real de um objeto fixo transladará .
II - Se um espelho plano girar de um ângulo q em torno de um eixo perpendicular à direção de incidência da luz, o raio refletido girará de um ângulo .
III - Para que uma pessoa de altura possa observar seu corpo inteiro em um espelho plano, a altura deste deve ser de no mínimo .
Então podemos dizer que:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$• \ \text{Afirmativa I:}$ $\color{royalblue}{\text{Verdadeira}}$
Numa representação da situação, temos:
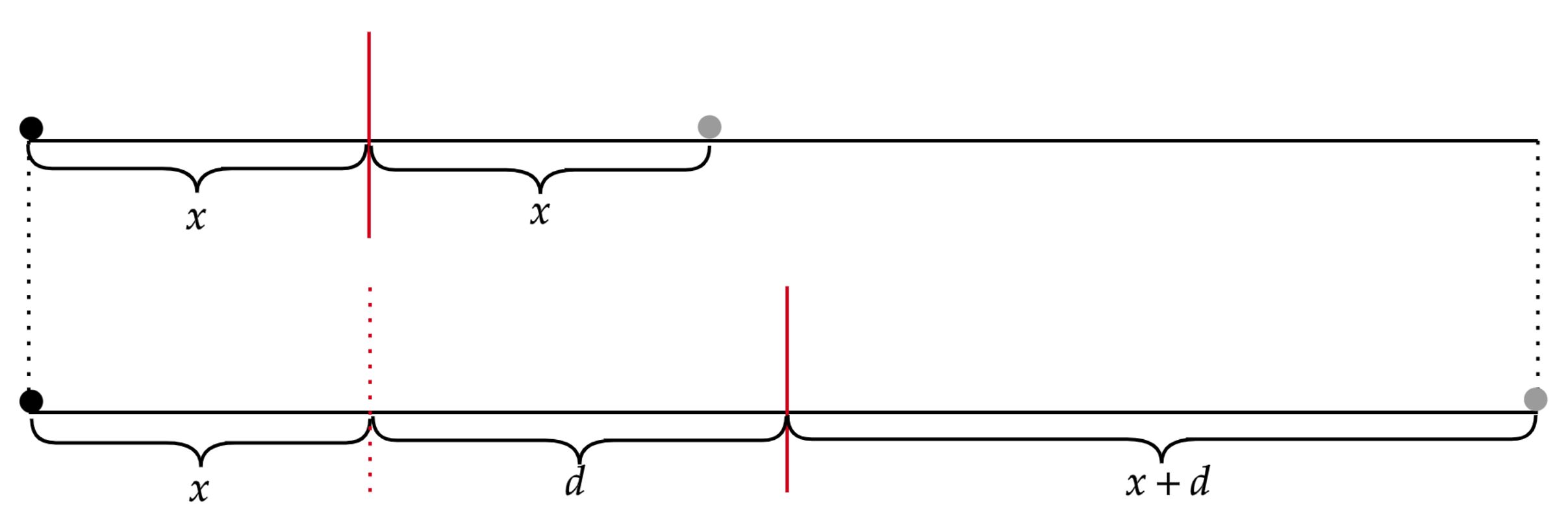 Veja que, a imagem do objeto fixo irá transladar $(\Delta S)$, escrito como:
\begin{matrix} \Delta S = 2(x+d) - 2(x) = 2d
\end{matrix}$• \ \text{Afirmativa II:}$ $\color{royalblue}{\text{Verdadeira}}$
O resultado em si é bem conhecido, mas podemos descobrir da seguinte maneira abaixo. Mas antes, veja que o ângulo de incidência "original" é $\theta$ e, após girar o espelho, teremos o ângulo $\alpha$, assim, o ângulo que girará o raio refletido será $\delta$. Continuando...
Veja que, a imagem do objeto fixo irá transladar $(\Delta S)$, escrito como:
\begin{matrix} \Delta S = 2(x+d) - 2(x) = 2d
\end{matrix}$• \ \text{Afirmativa II:}$ $\color{royalblue}{\text{Verdadeira}}$
O resultado em si é bem conhecido, mas podemos descobrir da seguinte maneira abaixo. Mas antes, veja que o ângulo de incidência "original" é $\theta$ e, após girar o espelho, teremos o ângulo $\alpha$, assim, o ângulo que girará o raio refletido será $\delta$. Continuando...
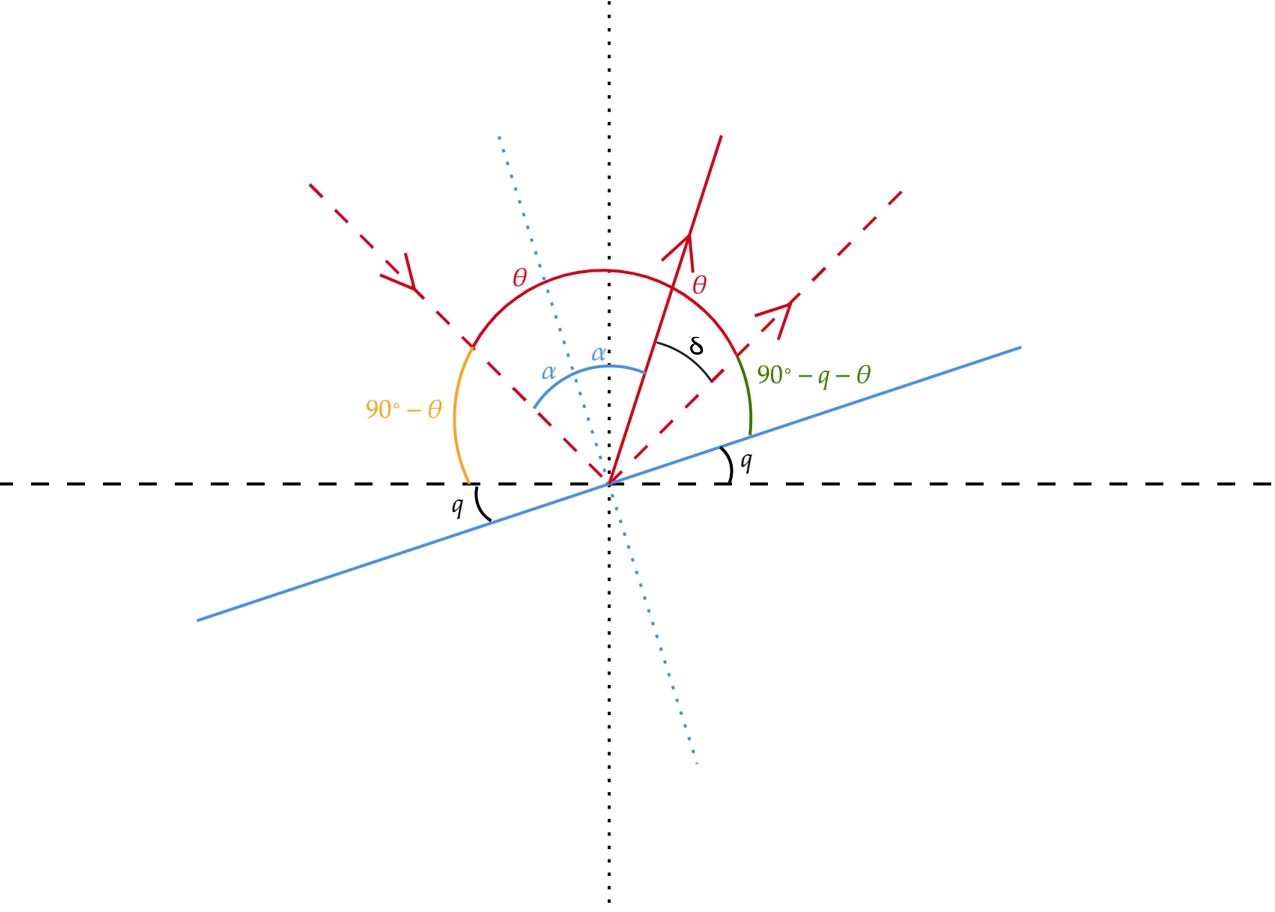 Repare que, resolveremos um sistema com duas equações, formadas pela soma de ângulos dando um ângulo reto, as quais são:
\begin{matrix} (1): &&& \alpha + \delta + (90^{\circ} - \theta - q) &=& 90^{\circ} \\ \\
(2): &&& \alpha + q+ (90^{\circ} - \theta ) &=& 90^{\circ}
\end{matrix}Não é difícil encontrar: $\fbox{$\delta = 2q$}$
$• \ \text{Afirmativa III:}$ $\color{orangered}{\text{Falsa}}$
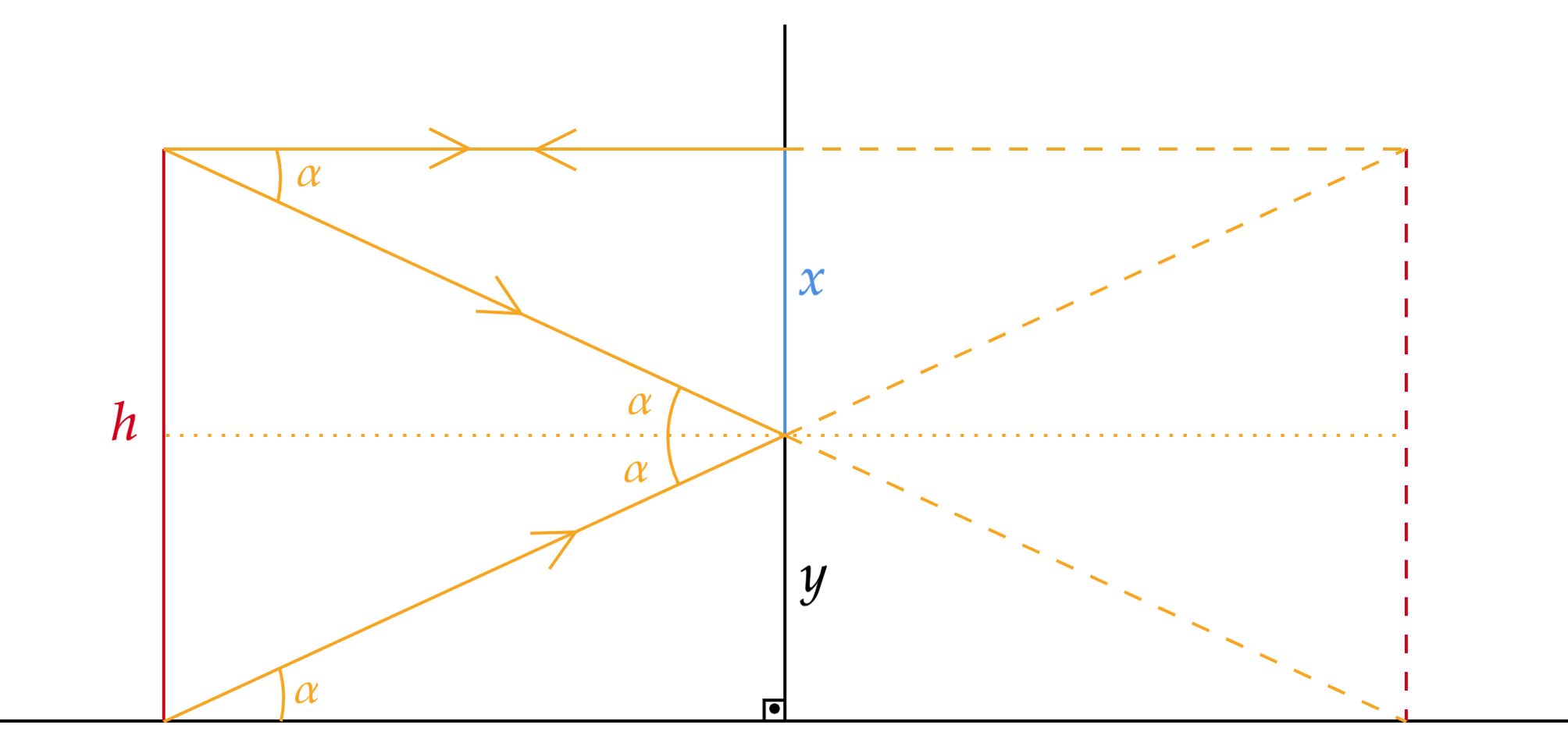
Novamente, repare o esboço abaixo, não é difícil perceber a congruência entre os triângulos por $A.L.A$ , a qual nos garante $x=y$. Dessa forma, na verdade, a altura deste deve ser de no mínimo $h/2$.
Repare que, resolveremos um sistema com duas equações, formadas pela soma de ângulos dando um ângulo reto, as quais são:
\begin{matrix} (1): &&& \alpha + \delta + (90^{\circ} - \theta - q) &=& 90^{\circ} \\ \\
(2): &&& \alpha + q+ (90^{\circ} - \theta ) &=& 90^{\circ}
\end{matrix}Não é difícil encontrar: $\fbox{$\delta = 2q$}$
$• \ \text{Afirmativa III:}$ $\color{orangered}{\text{Falsa}}$
Novamente, repare o esboço abaixo, não é difícil perceber a congruência entre os triângulos por $A.L.A$ , a qual nos garante $x=y$. Dessa forma, na verdade, a altura deste deve ser de no mínimo $h/2$.
 \begin{matrix} Letra \ (A)
\end{matrix}
\begin{matrix} Letra \ (A)
\end{matrix}

Ampliar Imagem

Ampliar Imagem

Ampliar Imagem
Analisando as afirmações temos que :
$\text{I)}$ Seja $x$ a translação realizada pela imagem devido a translação $d$ do espelho . A relação entre a velocidade $V_{e}$ do espelho no movimento de translação e a velocidade $V_{i}$ da imagem é dado por $V_{i} = 2V_{e}$ , realizando uma derivada em relação ao tempo podemos encontrar que $\dfrac{d(V_{i})}{dt} = \dfrac{d(2V_{e})}{dt} \implies \boxed{x = 2d}$ , concluindo dessa forma que essa afirmação é verdadeira.
$\text{II)}$ A relação entre o desvio $\alpha$ do raio refletido e a inclinação $\delta$ do espelho plano é dada por $\alpha = 2 \delta$ , se $\delta = q $ , então $\alpha = 2q$ , portanto , essa afirmação está correta.
$\text{III)}$ Essa afirmação está incorreta pois a altura mínima do espelho plano deve ser igual a $\dfrac{h}{2}$ para que a pessoa possa observar seu corpo por inteiro.
$\text{Resposta : Alternativa A}$


