Um capacitor plano é formado por duas placas paralelas, separadas entre si de uma distância , gerando em seu interior um campo elétrico uniforme . O capacitor está rigidamente fixado em um carrinho que se encontra inicialmente em repouso. Na face interna de uma das placas encontra-se uma partícula de massa e carga presa por um fio curto e inextensível. 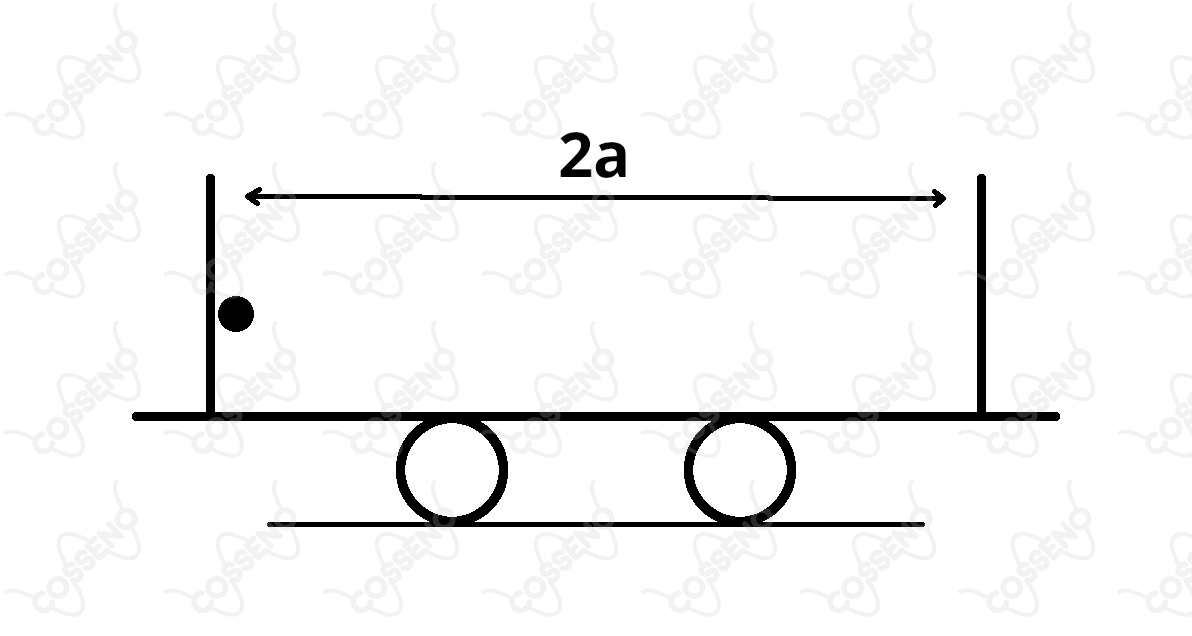
Considere que não haja atritos e outras resistências a qualquer movimento e que seja a massa do conjunto capacitor mais carrinho. Por simplicidade, considere ainda a inexistência da ação da gravidade sobre a partícula. O fio é rompido subitamente e a partícula move-se em direção à outra placa. A velocidade da partícula no momento do impacto resultante, vista por um observador fixo ao solo, é
CossenoGPT


