Uma partícula move-se ao longo de uma circunferência circunscrita em um quadrado de lado com velocidade angular constante. Na circunferência inscrita nesse mesmo quadrado, outra partícula move-se com a mesma velocidade angular. A razão entre os módulos das respectivas velocidades tangenciais dessas partículas é:
CossenoGPT
Teste
gratuitamente agora
mesmo! 
Esboçando a situação:
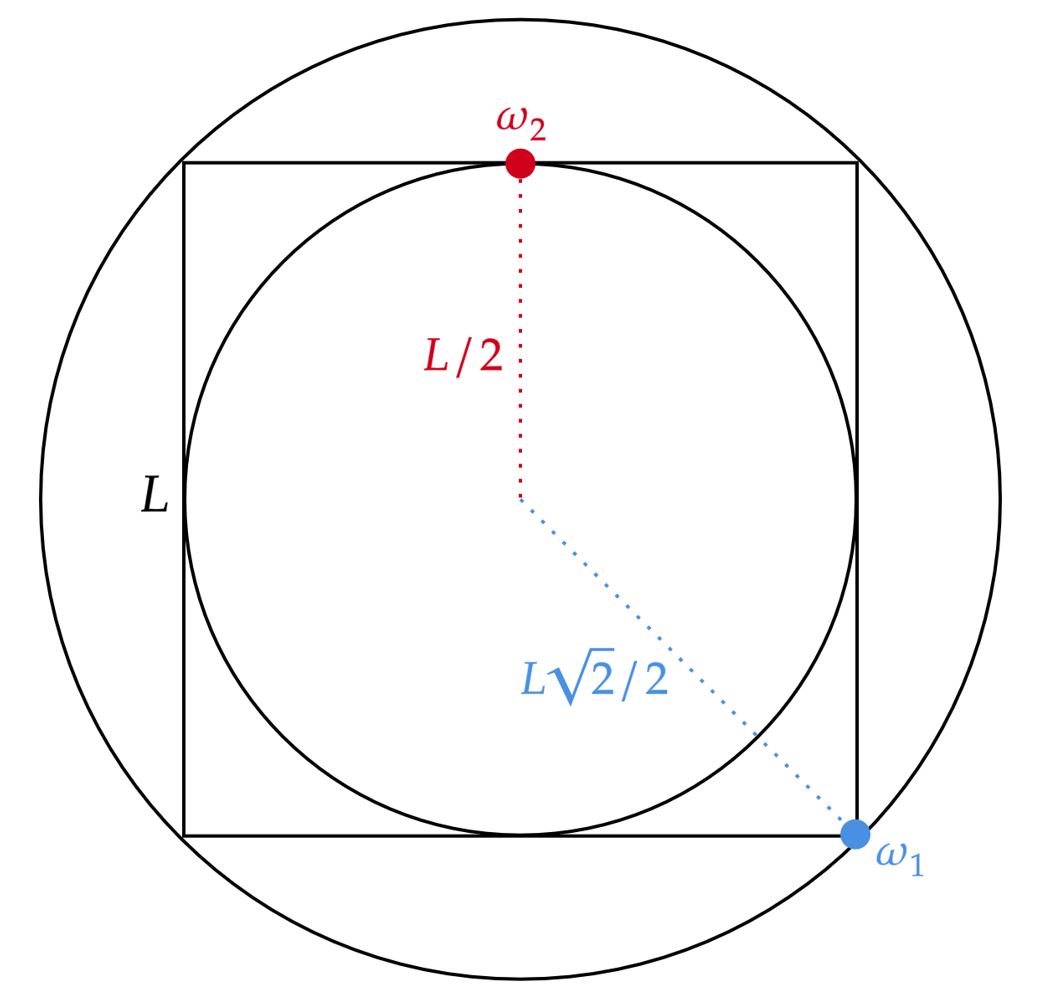Observe o enunciado, ele nos informa que as velocidades angulares são idênticas, então: \begin{matrix}
\omega_1 = \omega_2 &\Rightarrow& \dfrac{v_1}{r_1} = \dfrac{v_2}{r_2} &\Rightarrow& \dfrac{v_1}{v_2} = \dfrac{r_1}{r_2}
\end{matrix}Com isso, ao analisar a geometria do problema, pode-se encontrar os raios de curvatura como:\begin{matrix}r_1 = \dfrac{L\sqrt{2}}{2} &,& r_2 = \dfrac{L}{2}
\end{matrix}Portanto:\begin{matrix} \dfrac{v_1}{v_2} = \dfrac{\dfrac{L\sqrt{2}}{2} }{\dfrac{L}{2} } = \sqrt{2}
\end{matrix}\begin{matrix}Letra \ (A)
\end{matrix}
Ampliar Imagem
