A razão entre a área da base de uma pirâmide regular de base quadrada e a área de uma das faces é . Sabendo que o volume da pirâmide é de , temos que a altura da pirâmide mede (em metros):
CossenoGPT
Teste
gratuitamente agora
mesmo! 
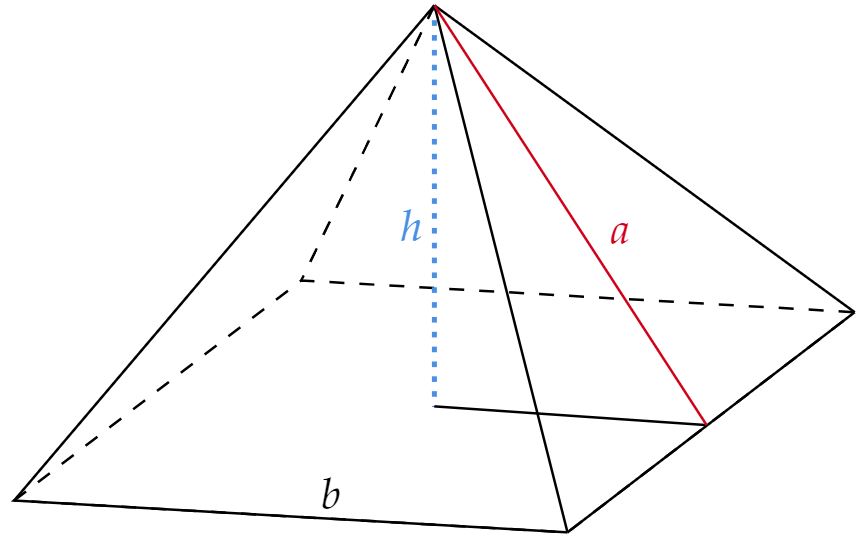
Denotemos a aresta da base de $b$, o apótema da pirâmide de $a$, e por fim, a altura de $h$. Nessa perspectiva, pela razão informada no enunciado, têm-se: \begin{matrix} {{\dfrac{b^2}{\left(\dfrac{b\cdot a}{2} \right)} }}= 2 &\therefore& b = a & (1)
\end{matrix}Analisando o triângulo retângulo formado pela altura, apótema da base $(\frac{b}{2})$ e apótema da pirâmide, têm-se: \begin{matrix} a^2 = h^2 + {{(\dfrac{b}{2})}}^2 &\therefore&b^2 = {{\dfrac{4}{3} }}h^2
\end{matrix}Por fim, pelo volume informado:\begin{matrix} {{\dfrac{h}{3}}} \cdot (b^2) = 12 &\Rightarrow& h^3 = 27 &\therefore& h = 3 \ \pu{m} & \tiny{\blacksquare}
\end{matrix}
\begin{matrix} Letra \ (C)
\end{matrix}
Ampliar Imagem
