A questão é relativamente simples caso se conheça um resultado notório para todo triângulo convexo, para isso, deve-se saber os conceitos de $\text{base média}$. Nesse contexto, vamos supor um triângulo de lados $(2a, 2b, 2c)$, tal que, ligando seus pontos médios, temos: 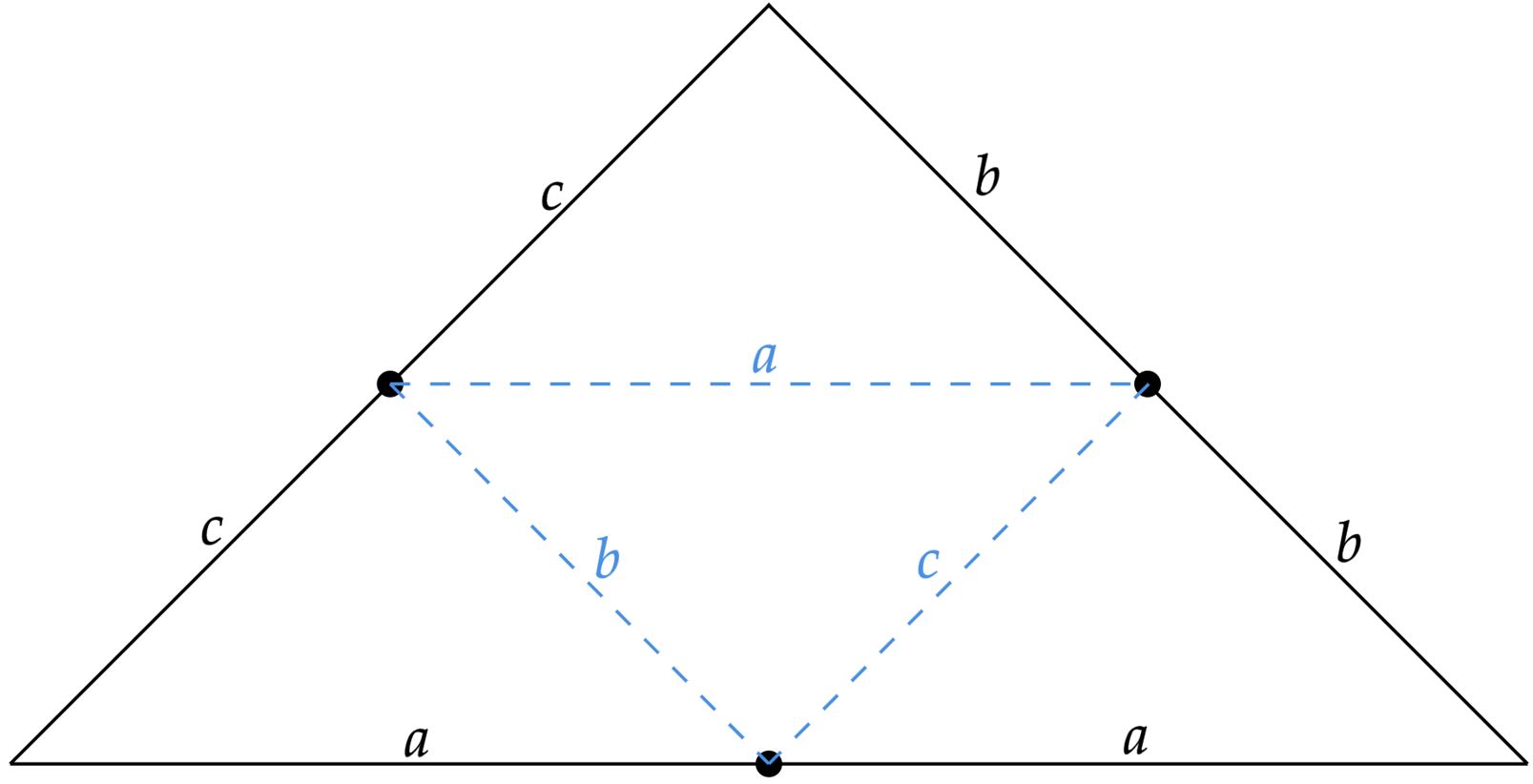Veja que, por critérios de $\text{Lado-Lado-Lado}$, todos os pequenos triângulos que compõem o grande triângulo são iguais, ou seja, se a área do grande triângulo é $S$, a do triângulo formado por seus pontos médios é $S/4$. Com isso, não é difícil perceber que estamos tratando de uma $\text{PG}$ na questão, esta que possui razão $q = 1/4$. No geral, o triângulo fornecido pelo enunciado é notório e comumente chamado de $\text{triângulo pitagórico}$, é um triângulo retângulo, em que podemos calcular sua área $S_1$ como:\begin{matrix} S_1 = \dfrac{4 \cdot 3}{2} = 6 \ \text{u.a} \end{matrix}Pensando agora na soma da $\text{PG}$, têm-se:\begin{matrix} \underset{i=1}{\overset{78}{\sum}} S_i &=& \dfrac{S_1 \cdot (1 - q^{78})}{1 - q} &=& \dfrac{6 \cdot \left( 1 - \dfrac{1}{4^{78}} \right)}{\dfrac{3}{4}} &\approx& \dfrac{6\cdot 4}{3} &=& 8 \ \text{u.a} \end{matrix}\begin{matrix}Letra \ (A) \end{matrix}$\color{orangered}{\text{Obs:}}$ $\left( 1 - \dfrac{1}{4^{78}} \right) \approx 1$