Pensando na situação descrita, pode-se imaginar um raio de luz sofrendo refração entre o ar e o filme. Adiante, pelo raio refratado, o caminho filme-lente representa a espessura do filme, caminha este que é metade da diferença de fase entre o raio que incide no filme e aquele que sai devido a reflexão na lente. Nesse sentido, vamos esboçar a situação: 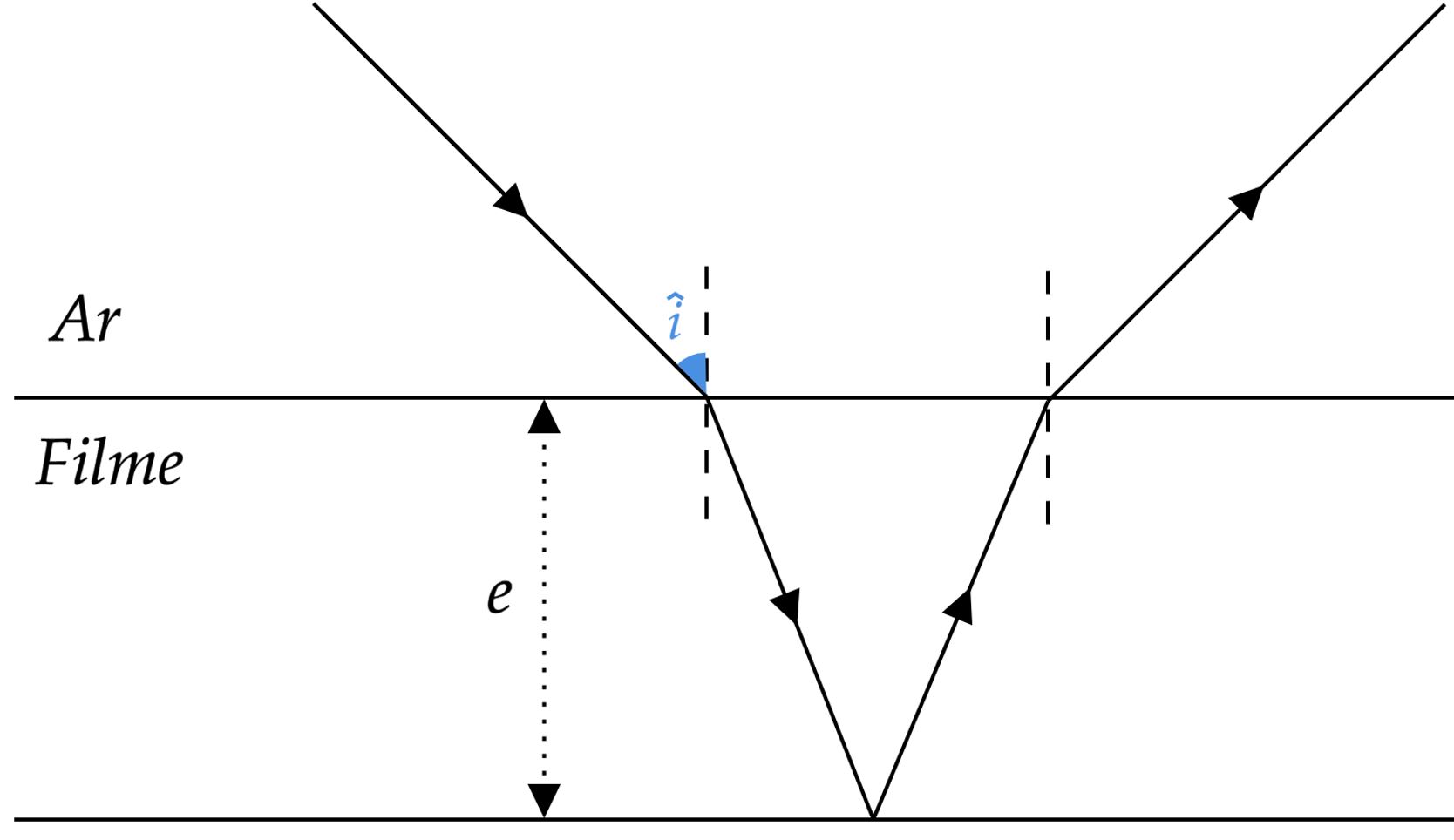Não se esqueça que o filme é fino e índice de refração é próximo do ar, ou seja, o ângulo de incidência $\hat{i}$ é próximo de $0$. Desse modo, para um ângulo tão pequeno, a diferença de caminho óptico $\Delta x$ é próxima de $2e$, em que podemos escrever:\begin{matrix} \Delta x = k \cdot \dfrac{\lambda_{\text{filme}}}{2} &\Rightarrow& e = k \cdot \dfrac{\lambda_{\text{filme}}}{4} \end{matrix}O comprimento de onda da luz no filme pode ser encontrado pela $\text{Lei de Snell}$, logo:\begin{matrix} \dfrac{\lambda_{\text{filme}}}{\lambda_{\text{ar}}} = \dfrac{n_{\text{ar}}}{n_{\text{filme}}} &\Rightarrow& \dfrac{\lambda_{\text{filme}}}{500} = \dfrac{1}{1,3} &\therefore& \lambda_{\text{filme}} = \dfrac{500}{1,3} \ \pu{nm} \end{matrix}Agora, nos resta pensar em $k$, este que é um número inteiro positivo, mas que depende da fase relativa entre os raios. Com isso, note que o raio incidente não sofre inversão de fase, porém, ao refletir na lente, este inverte a fase, saindo do filme com a fase invertida, visto que ele está partindo de um meio com índice de refração maior para um menor. Portanto, o raio que incide no filme e aquele que sai estão em oposição de fase, isto é, $k = 1,3,5,...$, como o filme é fino, é de se supor termos a menor diferença de comprimento, para isso, $k=1$, em que:\begin{matrix} e = 1 \cdot \dfrac{500}{1,3 } \cdot \dfrac{1}{4} &\therefore& e \approx 96 \ \pu{nm} \end{matrix}\begin{matrix}Letra \ (B) \end{matrix}