Certos resistores quando expostos à luz variam sua resistência. Tais resistores são chamados LDR (do inglês: “Light Dependent Resistor”). Considere um típico resistor LDR feito de sulfeto de cádmio, o qual adquire uma resistência de aproximadamente quando exposto à luz intensa, e de quando na mais completa escuridão. Utilizando este LDR e um resistor de resistência fixa para construir um divisor de tensão, como mostrado na figura, é possível converter a variação da resistência em variação de tensão sobre o LDR, com o objetivo de operar o circuito como um interruptor de corrente (circuito de chaveamento).
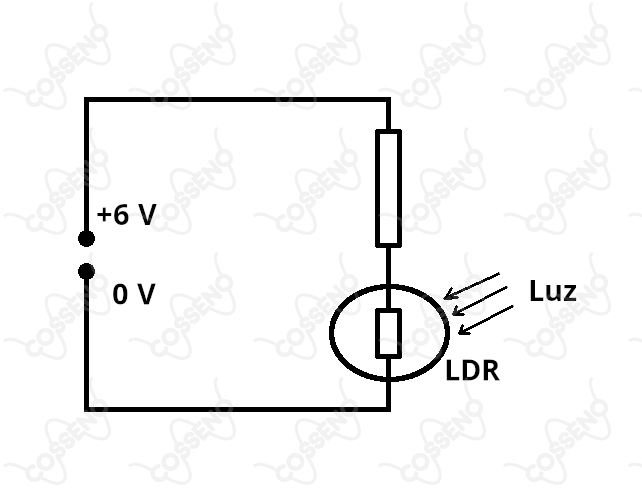
Para esse fim, deseja-se que a tensão através do LDR, quando iluminado, seja muito pequena comparativamente à tensão máxima fornecida, e que seja e valor muito próxima ao desta, no caso do LDR não iluminado. Qual dos valores de abaixo é o mais conveniente para que isso ocorra?
CossenoGPT


