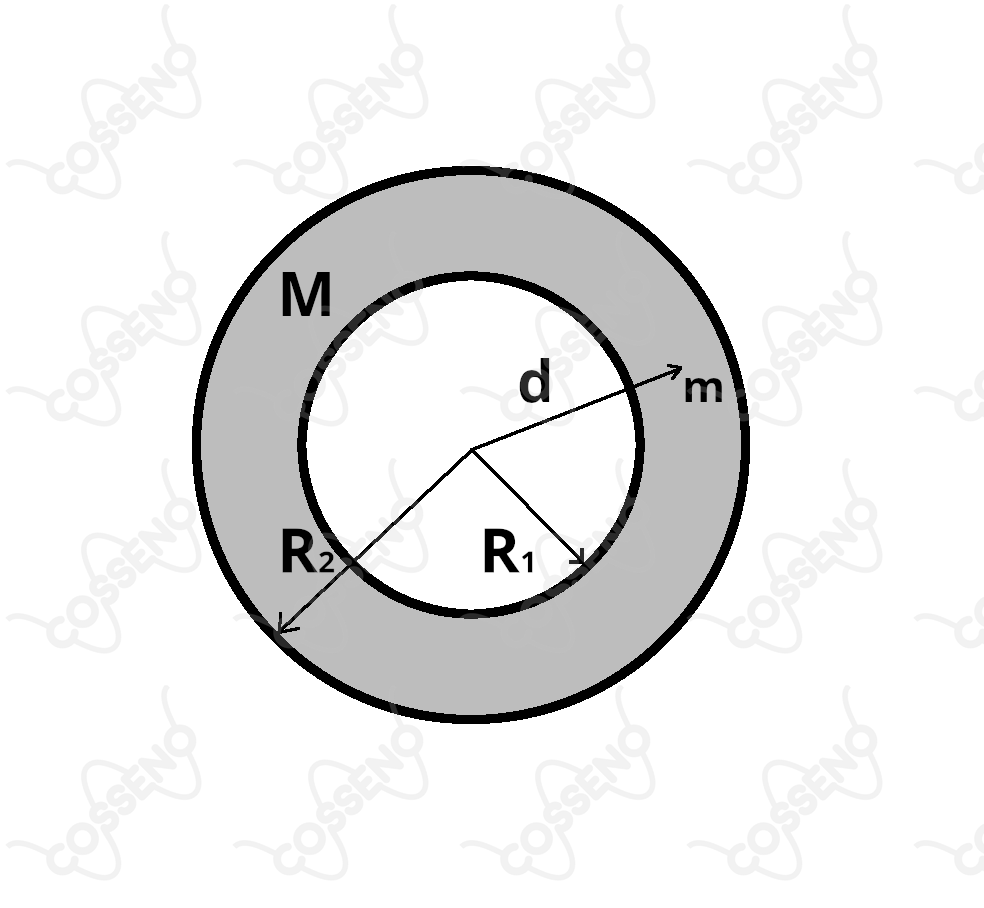
Uma casca esférica tem raio interno , raio externo e massa distribuída uniformemente. Uma massa puntiforme m está localizada no interior dessa casca, a uma distância d de seu centro (). O módulo da força gravitacional entre as massas é :
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Com conhecimento do teorema das cascas esféricas, mais precisamente que - uma esfera oca não exerce força gravitacional no seu interior - pode-se dizer que uma massa $M_c$ está atuando sobre a massa $m$. Veja abaixo:
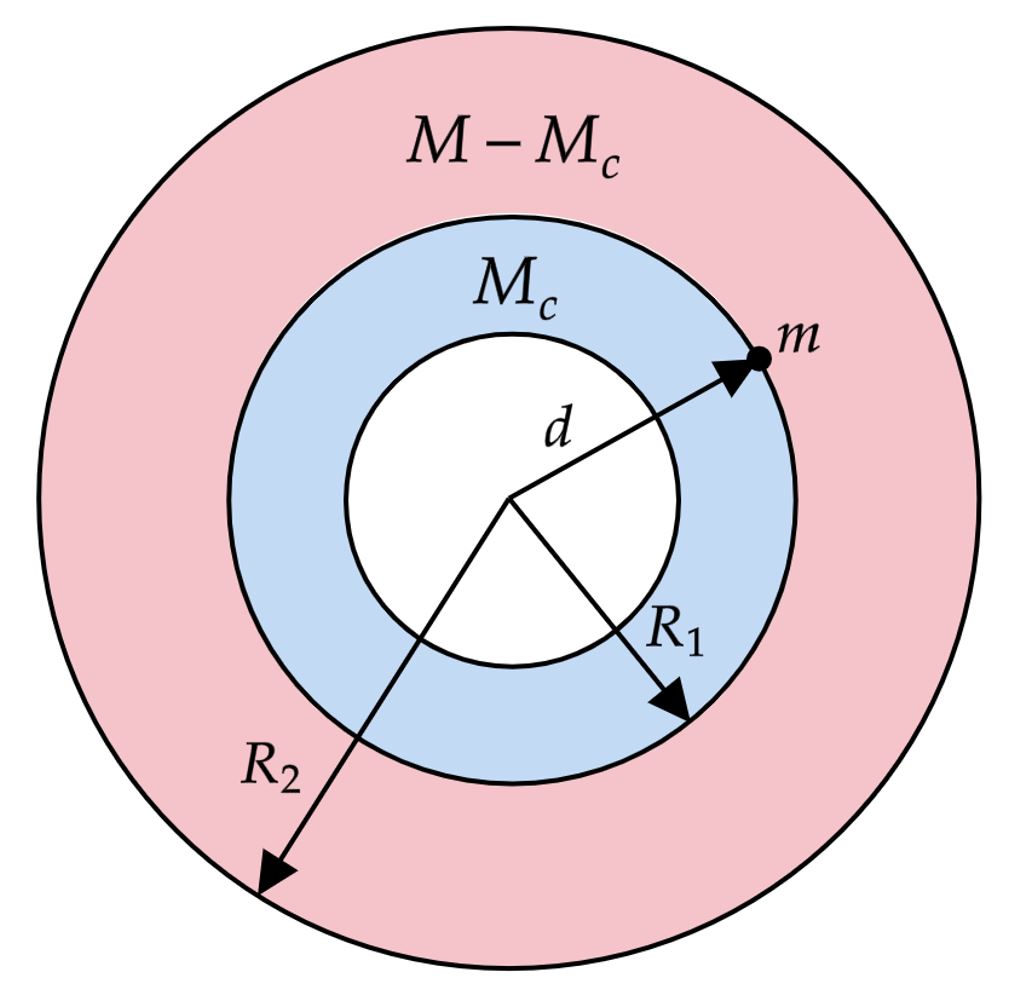 Nesse caso, vamos assumir que a densidade da casca seja $\rho$, então:\begin{matrix} M = \rho \cdot \dfrac{4}{3}\pi (R^3_2 - R^3_1) &,& M_c =\rho \cdot \dfrac{4}{3}\pi (d^3 - R^3_1)
\end{matrix}Assim,\begin{matrix}M_c = M \cdot \left( \dfrac{d^3 - R^3_1}{R^3_2 - R^3_1} \right)
\end{matrix}Com isso, a força gravitacional $F$ entre as massas é: \begin{matrix}
F = \dfrac{GM_c m}{d^2} &\therefore& F = \dfrac{GM m(d^3 - R^3_1)}{d^2(R^3_2 - R^3_1)} & \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (E)
\end{matrix}
Nesse caso, vamos assumir que a densidade da casca seja $\rho$, então:\begin{matrix} M = \rho \cdot \dfrac{4}{3}\pi (R^3_2 - R^3_1) &,& M_c =\rho \cdot \dfrac{4}{3}\pi (d^3 - R^3_1)
\end{matrix}Assim,\begin{matrix}M_c = M \cdot \left( \dfrac{d^3 - R^3_1}{R^3_2 - R^3_1} \right)
\end{matrix}Com isso, a força gravitacional $F$ entre as massas é: \begin{matrix}
F = \dfrac{GM_c m}{d^2} &\therefore& F = \dfrac{GM m(d^3 - R^3_1)}{d^2(R^3_2 - R^3_1)} & \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (E)
\end{matrix}

Ampliar Imagem

