Deixa-se cair continuamente areia de um reservatório a uma taxa de diretamente sobre uma esteira que se move na direção horizontal com velocidade .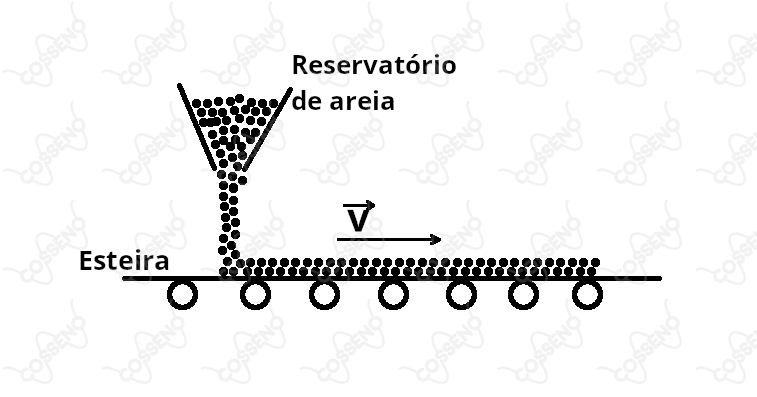
Considere que a camada de areia depositada sobre a esteira se locomove com a mesma velocidade , devido ao atrito. Desprezando a existência de quaisquer outros atritos, conclui-se que a potência em watts, requerida para manter a esteira movendo-se a , é:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Segundo enunciado, a taxa de areia cai diretamente sobre a esteira. Nesse viés, para que a esteira, assim como a massa de areia se movam com mesma velocidade, necessitamos que o par de forças entre as duas seja o mesmo, isto é, o atrito deve ser igual a força $F$ com que a esteira "empurra" os grãos de areia. Com isso, pela segunda lei de Newton, têm-se: \begin{matrix}
F = \dfrac{\Delta p}{\Delta t} &,& p = mV &\Rightarrow&F = \underset{3,0 \ \pu{kg/s}} {\boxed{\dfrac{\Delta m}{\Delta t}}} \cdot V &,& V = 4,0 \ \pu{m/s} &\therefore& F = 12 \ \pu{N}
\end{matrix}Sobre a potência, podemos analisar o trabalho realizado pela força $F$, ou seja: \begin{matrix} Pot = \dfrac{F \cdot d}{\Delta t} &,& \dfrac{ d}{\Delta t} = V &\therefore& Pot = 48 \ \pu{W} &\tiny{\blacksquare}
\end{matrix}
\begin{matrix} Letra \ (E)
\end{matrix}

