A figura abaixo representa um sistema experimental utilizado para determinar o volume de um líquido por unidade de tempo que escoa através de um tubo capilar de comprimento e seção transversal de área .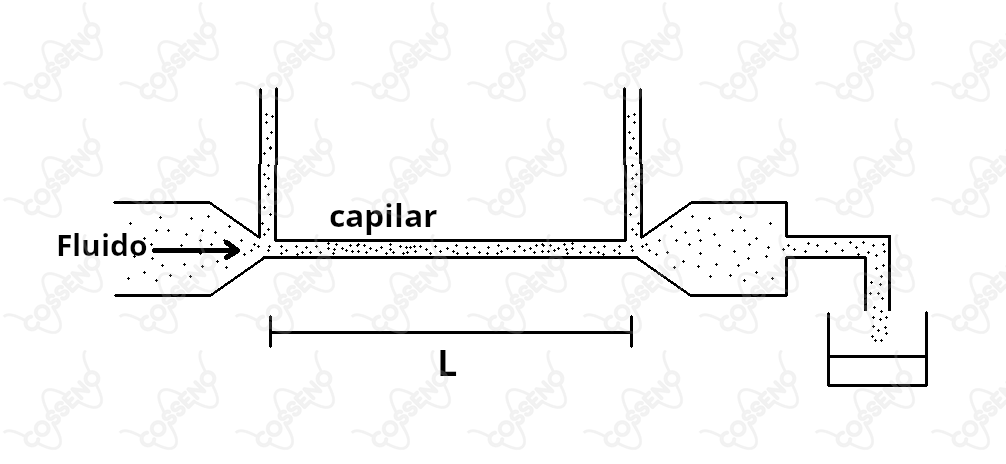
Os resultados mostram que a quantidade desse fluxo depende da variação da pressão ao longo do comprimento do tubo por unidade de comprimento , do raio do tubo () e da viscosidade do fluido () na temperatura do experimento. Sabe-se que o coeficiente de viscosidade () de um fluido tem a mesma dimensão do produto de uma tensão (força por unidade de área) por um comprimento dividido por uma velocidade.
Recorrendo à análise dimensional, podemos concluir que o volume de fluido coletado por unidade de tempo é proporcional a:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A princípio, podemos escrever: \begin{matrix}
\Phi \propto \left(\dfrac{\Delta P}{L} \right)^x \cdot (a)^y \cdot (\eta)^z &,& [\Phi] = \dfrac{L^3}{T}
\end{matrix}Com isso, vamos começar realizando a análise dos componentes da proproção, em que: \begin{matrix}
\Delta P = \dfrac{F}{A} &\Rightarrow& [\Delta P] = \dfrac{M}{L \cdot T^2} &\therefore& \left[\dfrac{\Delta P}{L} \right] = \dfrac{M}{L^2 \cdot T^2}
\end{matrix}Analogamente, para viscosidade, o enunciado contribui dizendo:\begin{matrix}
\eta = \dfrac{F}{A} \cdot \dfrac{L}{v} &\Rightarrow& \left[\eta \right] = \dfrac{M}{L \cdot T}
\end{matrix}Já podemos substituir nossos resultados, tal que:\begin{matrix}
\dfrac{L^3}{T} = \left(\dfrac{M}{L^2 \cdot T^2} \right)^x \cdot (L)^y \cdot \left(\dfrac{M}{L \cdot T}\right)^z = \dfrac{M^{x+z} \cdot L^{y-2x-z}}{T^{2x+z}}
\end{matrix}Dessa maneira, encontramos um sistema de equações, veja: \begin{matrix}\begin{cases}
\ \ \ \ \ x+z &=& 0 \\
\ \ \ 2x + z&=& 1 \\
y-2x-z &=& 3
\end{cases} &\Rightarrow& x =1 &,& z = -1 &,& y = 4
\end{matrix}Portanto,\begin{matrix}
\Phi \propto \left(\dfrac{\Delta P}{L} \right) \cdot \dfrac{a^4}{\eta}
\end{matrix}\begin{matrix}Letra \ (B)
\end{matrix}

