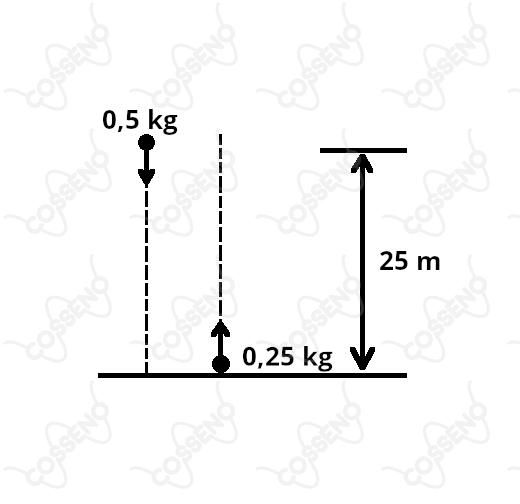
Uma bola de é abandonada a partir do repouso a uma altura de acima do chão. No mesmo instante, uma segunda bola, com massa de , é lançada verticalmente para cima, a partir do chão, com velocidade inicial de . As duas bolas movem-se ao longo de linhas muito próximas, mas que não se tocam. Após segundos, a velocidade do centro de massa do sistema constituído pelas duas bolas é de:
Primeiro é necessário adotar um sentido para o movimento, como tudo ocorre na vertical, tanto a queda quanto o lançamento (por conseguinte o centro de massa), adotemos o movimento $para \ cima \ como \ positivo$.
• Calculando a Velocidade da Bola que está caindo $(V = V_0 + a.\Delta T)$
\begin{matrix} ?V_1 = 0 - 10\cdot 2 \rightarrow V_1 = 20 \ \pu{m/s} \ (para \ baixo) \end{matrix}
• Calculando a Velocidade da Bola que foi jogada para cima $(V = V_0 + a\cdot \Delta T)$
\begin{matrix} ?V_2 = 15 - 10\cdot 2 \rightarrow V_1 = 5 \ \pu{m/s} \ (para \ baixo) \end{matrix}
Note que como não sabia o sentido de $V_2$ e $V_1$, coloquei $?$, pois a partir do sinal seria possível encontrar o sentido, visto que adotamos o movimento para cima como positivo, o sinal negativo indica o movimento para baixo.
• Velocidade do Centro de Massa $(V_{cm} = \dfrac{m_1\cdot V_1 + m_2\cdot V_2}{m_1 + m_2})$
\begin{matrix} V_{cm} = {{\dfrac{-0,50\cdot 20 - 0,25\cdot 5}{0,50 + 0,25}}} &\Rightarrow & V_{cm} = - 15 \ \pu{m/s} \ (para \ baixo) \end{matrix}\begin{matrix} Letra \ (C)
\end{matrix}
