Uma lâmina de material muito leve de massa está em repouso sobre uma superfície sem atrito. A extremidade esquerda da lâmina está a de uma parede. Uma formiga considerada como um ponto, de massa , está inicialmente em repouso sobre essa extremidade, como mostra a figura.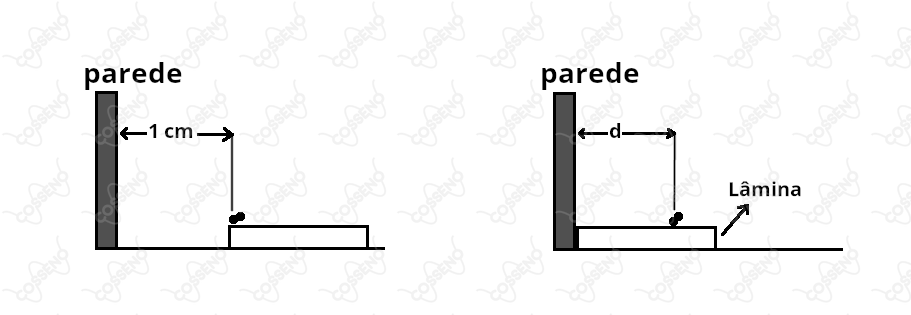
A seguir, a formiga caminha para frente muito lentamente, sobre a lâmina. A que distância da parede estará a formiga no momento em que a lâmina tocar a parede?
CossenoGPT
Teste
gratuitamente agora
mesmo! 
A princípio, vamos supor um sistema isolado, isto é, assumir a conservação da quantidade de movimento. Nesse contexto, podemos pensar em coordenadas num eixo horizontal, em que se a lâmina apresentar comprimento $2l$, podemos esboçar:
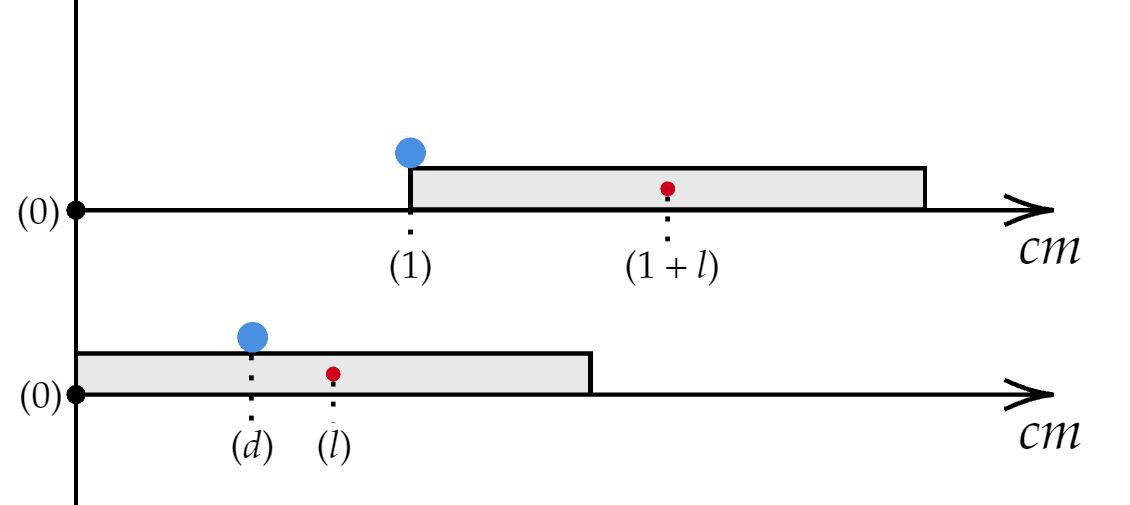Aplicando a conservação da quantidade de movimento:\begin{matrix}
\Delta \vec{p} = 0 &\Rightarrow& \dfrac{m}{5} \cdot \vec{V}_f + m \cdot \vec{V}_l = 0
\end{matrix}Com isso, vamos supor que tudo ocorra num intervalo de tempo $\Delta t$, em que a formiga andou $\Delta x_f$ e a lâmina percorreu $\Delta x_l$. Desse modo, multiplicando a expressão acima por $\Delta t$ e dividindo por $m$, têm-se:\begin{matrix}\dfrac{1}{5} \cdot \Delta x_f + \Delta x_l= 0
\end{matrix}Em que,\begin{matrix}
\Delta x_f = d - 1 &,& \Delta x_l = l - (1+l)
\end{matrix}Então,\begin{matrix}\dfrac{1}{5} \cdot (d-1) + (-1)= 0 &\therefore& d = 6 \ \pu{cm} &\tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (E)
\end{matrix}
Ampliar Imagem
A questão fala que a superfície cuja lâmina está apoiada não tem atrito, logo, se algo (a formiga) andar pra direita, a lâmina vai se movimentar para o lado contrário ( esquerda, de encontro com a parede).
Se a formiguinha tem 1/5 da massa da lâmina em questão, a lâmina vai andar 1 cm para a esquerda quando a formiguinha andar o Quíntuplo para a direita. se ela já estava com a distancia de 1 cm da parede (Do = Distancia Original), só é necessário somar o que ela andou (Dp = Distancia percorrida) com Do, originando a Distancia Total (Dt):
Do + Dp = Dt
1cm + (1*5) cm = Dt
1cm + 5cm =Dt
6 cm = Dt
