Quatro lâmpadas idênticas 1, 2, 3 e 4, de mesma resistência , são conectadas a uma bateria com tensão constante , como mostra a figura.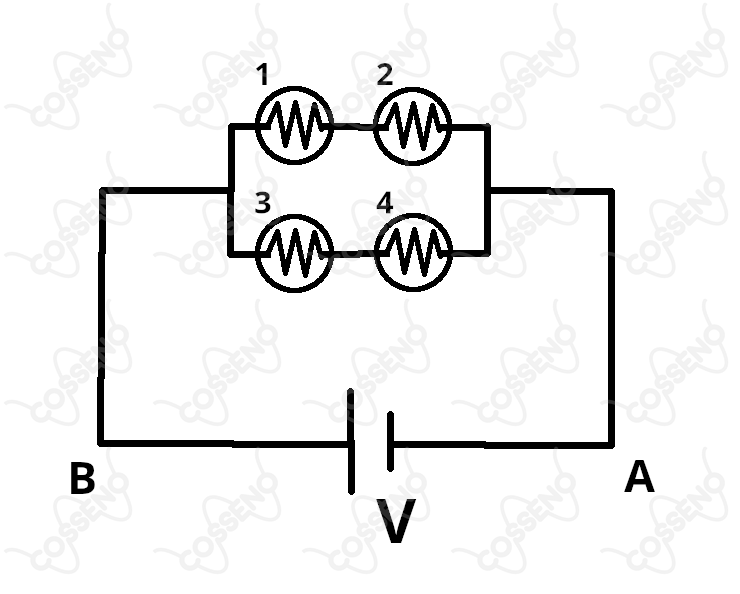
Se a lâmpada 1 for queimada, então:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A priori, na situação em que nenhuma lâmpada foi queimada, pode-se perceber que as resistências equivalentes de cada ramo são iguais, isto é, a corrente que passa em cima é a mesma que passa em baixo, denotemos ela de $i_1$. Nessa perspectiva, a partir da $\text{Primeira Lei de Ohm}$, têm-se a relação:\begin{matrix} V = 2R\cdot i_1 &\therefore& i_1 = {\dfrac{V}{2R}}
\end{matrix}Nesse viés, sendo $i$ a intensidade da corrente resultante entre $A$ e $B$, não é difícil perceber que ela é $\fbox{$i = 2i_1$}$.
Após a lâmpada $1$ queimar, o circuito de cima abre, quer dizer, não passa mais corrente nesse ramo, sendo a lâmpada $2$ consequentemente apagada. Com isso, a resistência equivalente passa a ser uma associação em série das lâmpadas $3$ e $4$, assim: \begin{matrix} V = 2R\cdot i_2 &\therefore& i_2 = {\dfrac{V}{2R}} &\Rightarrow& \fbox{$ i_2 = i_1$}
\end{matrix}Constata-se então que a corrente entre $A$ e $B$ cai pela metade, logo, nos resta apenas descobrir o que acontece com a lâmpada $3$, vejamos cada caso: \begin{matrix} \text{Inicial:} & Pot = R\cdot (i_1)^2 && \text{Final:} & Pot = R\cdot (i_2)^2
\end{matrix}Dessa forma, o brilho da lâmpada $3$ permanece constante. Além de claro, a potência drenada da bateria cair pela metade, visto que a corrente cai pela metade. \begin{matrix} Letra \ (E)
\end{matrix}

