Esboçando a situação, temos: 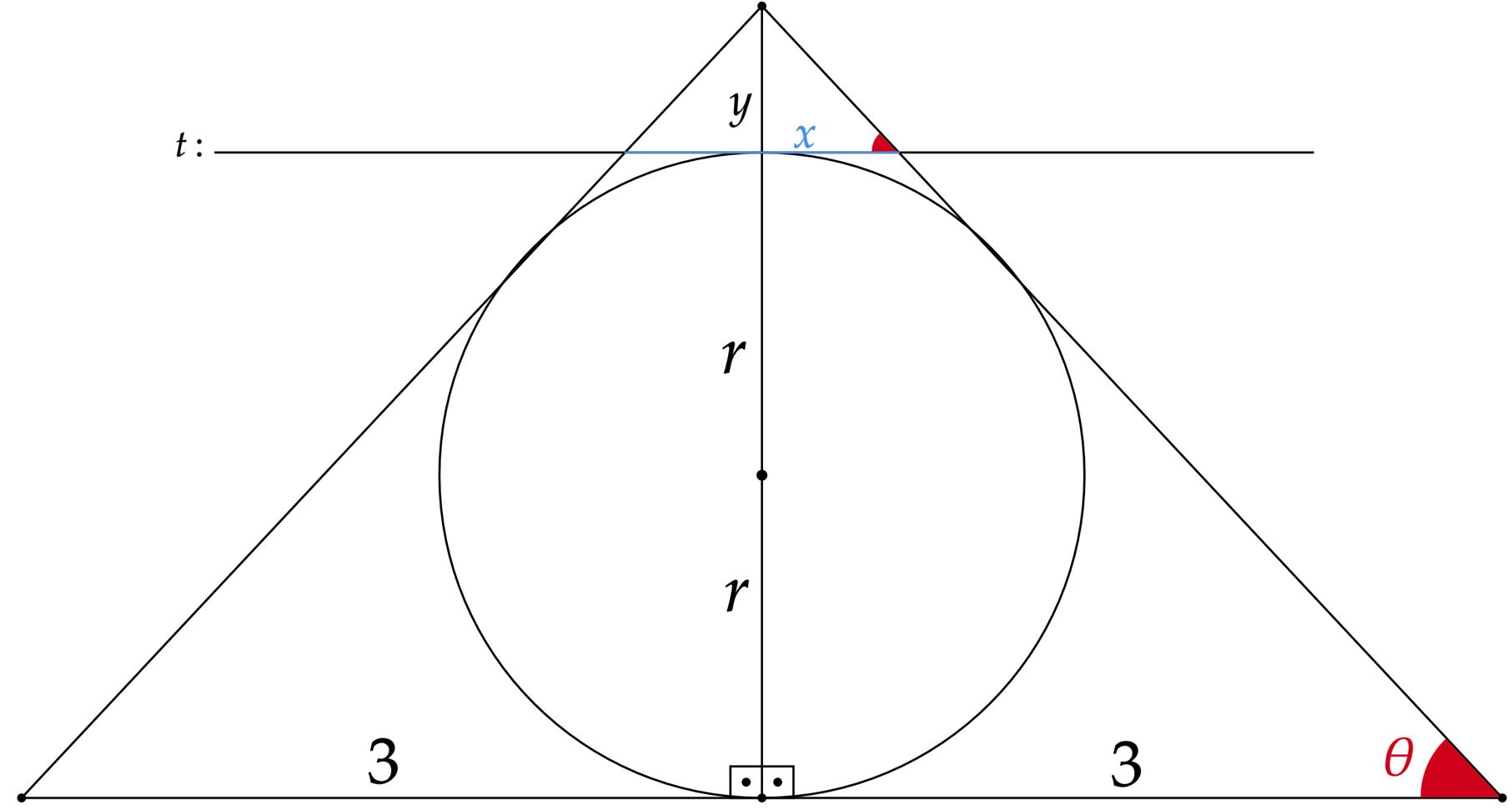Nesse contexto, não é difícil aplicar Pitágoras num dos triângulos e encontrar as hipotenusas, assim, podemos encontrar o raio do círculo a partir de uma relação entre áreas, veja: \begin{matrix} \dfrac{4 \cdot 6}{2} = r \cdot \underbrace{\left( \dfrac{5+5+6}{2} \right)}_{\text{semi-perímetro}} &\therefore& r = \dfrac{3}{2} \ \pu{cm} \end{matrix}Desse modo, pode-se encontrar a distância $x$ que pertence ao segmento $t$ como: \begin{matrix} \tan{\theta} = \dfrac{4}{3} = \dfrac{y}{x} &|& 2r + y = 4 &\Rightarrow& y = 1 \ \pu{cm} &\therefore& x = \dfrac{3}{4} \ \pu{cm} \end{matrix}Como o segmento todo vale $2x$, este deve ser igual a: $\boxed{1,5 \ \pu{cm}}$\begin{matrix}Letra \ (B) \end{matrix}