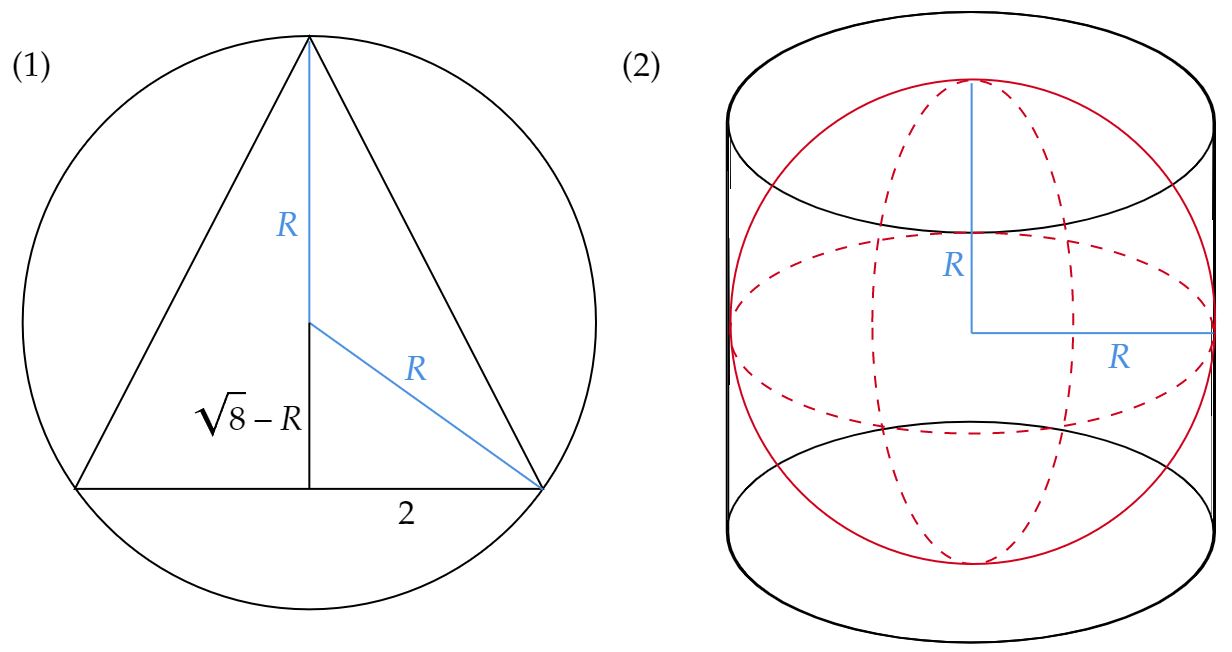
Comecemos denotando a geratriz do cone de $g$, por Pitágoras, têm-se: \begin{matrix} g^2 = (\sqrt{8})^2 + 2^2 &\therefore& g = 2\sqrt{3} \ \pu{ cm} \end{matrix}Com isso, a área lateral total do cone é: \begin{matrix} A_{Cone} = \pi(2)^2 +\pi(2)(g) &\therefore& A_{Cone} = 4\pi (\sqrt{3} + 1) \ \pu{cm^2} \end{matrix}Veja que, o problema trata da inscrição de sólidos, assim, trabalhemos em pares, isto é, começar analisando o cone inscrito na esfera. Nesse viés, planificando a situação, temos a figura $(1)$ abaixo, dela, $R$ é o raio da esfera, então por Pitágoras: \begin{matrix} R^2 = (\sqrt{8} - R)^2 + 2^2 &\therefore& R = {{\dfrac{3\sqrt{2}}{2} } } \ \pu{ cm} \end{matrix}Agora, pensando na esfera inscrita no cilindro - figura $(2)$ - a altura do cilindro é duas vezes o raio da esfera, e obviamente o raio da base do cilindro também é o raio da esfera. Desse modo, a área lateral total do cilindro é: \begin{matrix} A_{Cilindro} = 2(\pi R^2) +2\pi(R)(2R) &\Rightarrow&A_{Cilindro} = 6\pi R ^2&\therefore& A_{Cilindro} = 27\pi \ \pu{ cm^2} \end{matrix}Portanto, a razão solicitada: \begin{matrix} {{ \dfrac{A_{Cilindro} }{A_{Cone} } }} = {{\dfrac{27}{8}}} \cdot (\sqrt{3} - 1) & \tiny{\blacksquare} \end{matrix} \begin{matrix} Letra \ (D) \end{matrix}