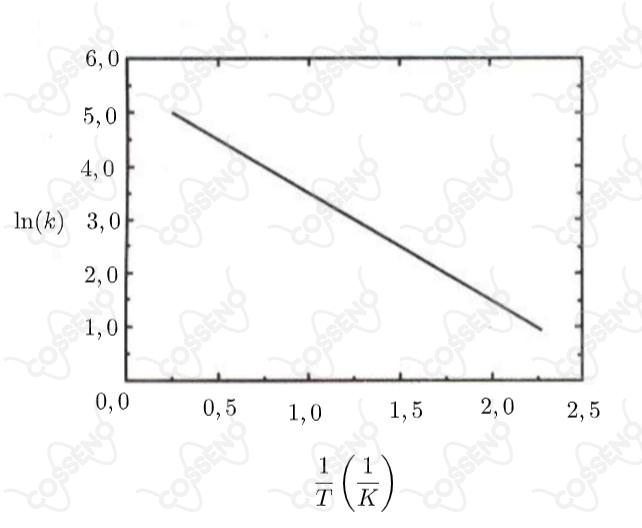
A equação de Arrhenius mostra a relação de dependência da constante de velocidade () de uma reação química com a temperatura (), em kelvin (), a constante universal dos gases (), o fator pré-exponencial () e a energia de ativação (). A curva abaixo mostra a variação da constante de velocidade com o inverso da temperatura absoluta para uma dada reação química que obedece à equação acima. A partir da análise deste gráfico, assinale a opção que apresenta o valor da razão para essa reação.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A partir da equação de Arrhenius, aplicando o logaritmo natural: \begin{matrix} \ln{k} &=& \ln{A.e^{-E_a/RT}} &=& \ln{A} \ - \ \ln{e^{E_a/RT}} &=& \ln{A} - {{\dfrac{E_a}{RT}}}
\end{matrix}Assim, veja a similaridade da reta do gráfico e a equação abaixo: \begin{matrix} \ln{k} &=& -{{\dfrac{E_a}{R}}}\cdot {{\dfrac{1}{T}}} &+& \ln{A}
\end{matrix}Atente que, o coeficiente angular da reta $(\tan{\alpha})$ do gráfico será numericamente igual a $\left(-{{\dfrac{E_a}{R}}}\right)$, veja: \begin{matrix}\tan{(180^{\circ} -\alpha)} = {{\dfrac{(5-1)}{(2,25 - 0,25)}}} = 2
\end{matrix}Continuando, \begin{matrix} \tan{\alpha} = -2 &\therefore& \fbox{${{\dfrac{E_a}{R}}} = 2,0$}
\end{matrix} \begin{matrix} Letra \ (E)
\end{matrix} $\color{orangered}{\text{Nota:}}$ O fator pré-exponencial é numericamente igual a um.\begin{matrix} \tan{\alpha} = {{\dfrac{\ln{k}}{\left( {\dfrac{1}{T}} \right)}}} = -2 &\Rightarrow& \ln{k} =-2 \cdot {{\dfrac{1}{T}}} &\therefore& \ln{A} = 0 &\Rightarrow& A = 1 \ \tiny{\blacksquare}
\end{matrix}

