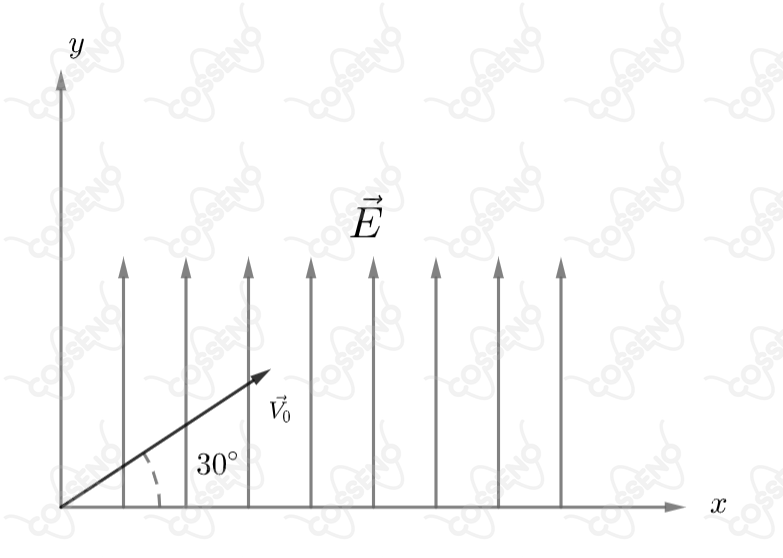
No instante , um elétron é projetado em um ângulo de em relação ao eixo , com velocidade de , conforme o esquema abaixo. Considerando que o elétron se move num campo elétrico constante , o tempo que o elétron levará para cruzar novamente o eixo é de:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Com conhecimento de que: \begin{matrix} m_e \approx 9,1 \cdot 10^{-34} \ \pu{kg} &,& e^{-} \approx 1,6\cdot 10^{-19} \ \pu{C}
\end{matrix}Como o elétron apresenta carga negativa, e o campo elétrico está no sentido positivo de $y$, vertical para cima, sabemos que a força elétrica atuará para baixo, logo: \begin{matrix} |F_e|=|F_r| &\Rightarrow& E\cdot e = m_e\cdot a &\Rightarrow& \fbox{$a=\dfrac{E\cdot e}{m_e}$}
\end{matrix}Ao decompor a velocidade inicial para analisar o movimento vertical: \begin{matrix} V_{0y} = V_0\sin{30^{\circ}}
\end{matrix}Calculando o tempo de subida, e eventualmente de descida: \begin{matrix} V_y = V_{0y} + (-a)t &\Rightarrow& 0 =V_0\sin{30^{\circ}} -\dfrac{E\cdot e}{m_e}t &\Rightarrow& t = {\dfrac{V_0\sin{30^{\circ}}\cdot m_e}{E\cdot e}}
\end{matrix} Não se esqueça que queremos o momento em que o elétron volta a cruzar o eixo $x$, isso significa subir e descer, assim temos:\begin{matrix} T= 2t = 2 \cdot \dfrac{V_0\sin{30^{\circ}}\cdot m_e}{E\cdot e}
\end{matrix}Substituindo os valores, podemos encontrar: \begin{matrix} T \approx 23\cdot 10^{-9} \ \pu{s} &\Rightarrow& \fbox{$T = 23 \ \pu{ns}$} \\ \\ & Letra \ (C)
\end{matrix}

21:01 12/11/2024
pq o problema nao fala nada de gravidade, e a unica força que gera aceleraçao no eixo Y é a força eletrica, logo a aceleraçao em y depende do campo

19:52 05/01/2023
Pq desconsiderar a gravidade? E apenas dizer que a aceleração gerada no corpo vem apenas do campo elétrico?


