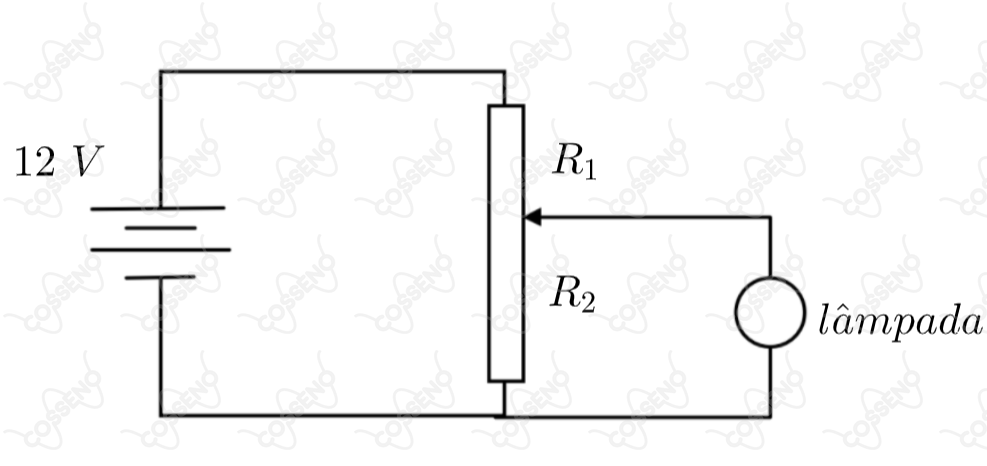
A força eletromotriz (f.e.m.) da bateria do circuito abaixo de . O potenciômetro possui uma resistência total de e pode ser percorrido por uma corrente máxima de . As correntes que devem fluir pelos resistores e , para ligar uma lâmpada projetada para funcionar em e , são, respectivamente:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A priori, deve-se admitir que a lâmpada funcione com suas respectivas especificações. Nesse contexto, podemos descobrir a corrente que deve passar por ela, para isso, utilizemos a potência da lâmpada:\begin{matrix} Pot = i_L \cdot \Delta V &\Rightarrow& 3 = i_L \cdot 6 &\therefore& i_L = 0,5 \ \pu{A}
\end{matrix}Observe que, por condições da lâmpada, o potencial através da resistência $R_1$ é a mesma que da resistência $R_2$, ou seja, $6 \ \pu{V}$. Com isso, vamos supor que bateria forneça uma corrente $i$, com conhecimento da $\text{Primeira Lei de Ohm}$, têm-se:\begin{matrix}\begin{cases}
\ \ \ \ \ \ R_1 \cdot i &=& 6 \\ R_2 \cdot (i -i_L) &=& 6
\end{cases}&\Rightarrow& R_1 + R_2 = \dfrac{6}{i} + \dfrac{6}{i - 0,5} = 15 &\Rightarrow& \underbrace{10i^2 - 9i - 2 = 0}_{\Delta \ = \ 161}
\end{matrix}Continuando,\begin{matrix}i = \dfrac{9 \pm \sqrt{161}}{2 \cdot 10} &,& \sqrt{161} \approx 13 &\therefore& i \approx 1,1 \ \pu{A}
\end{matrix}Portanto, como a corrente que passa em $R_1$ é $i - i_L$ e, em $R_2$ é $i$, constatamos:\begin{matrix}Letra \ (D)
\end{matrix}

