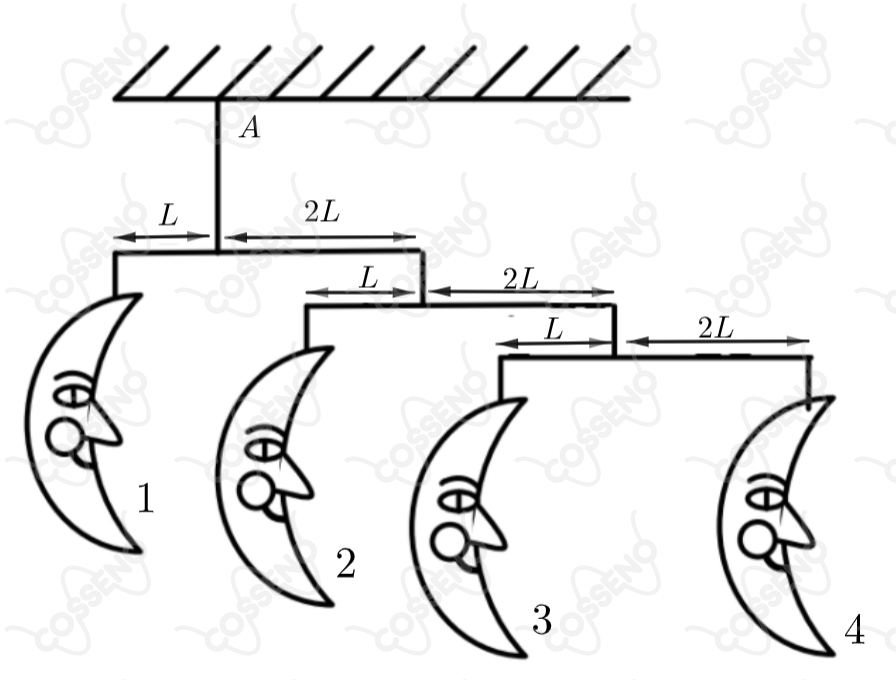
Um brinquedo que as mamães utilizam para enfeitar quartos de crianças é conhecido como “mobile”. Considere o “mobile” de luas esquematizado na figura abaixo. As luas estão presas por meio de fios de massas desprezíveis a três barras horizontais, também de massas desprezíveis . O conjunto todo está em equilíbrio e suspenso num único ponto . Se a massa da lua é de , então a massa em quilograma da lua é:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Como todo o conjunto está em equilíbrio, podemos fazer a análise de duas partas até, para isso, pode-se começar pelo pequeno sistema formado pelas luas 3 e 4. No caso, por simplificação, vamos esboçar as luas como bolinhas, em que:
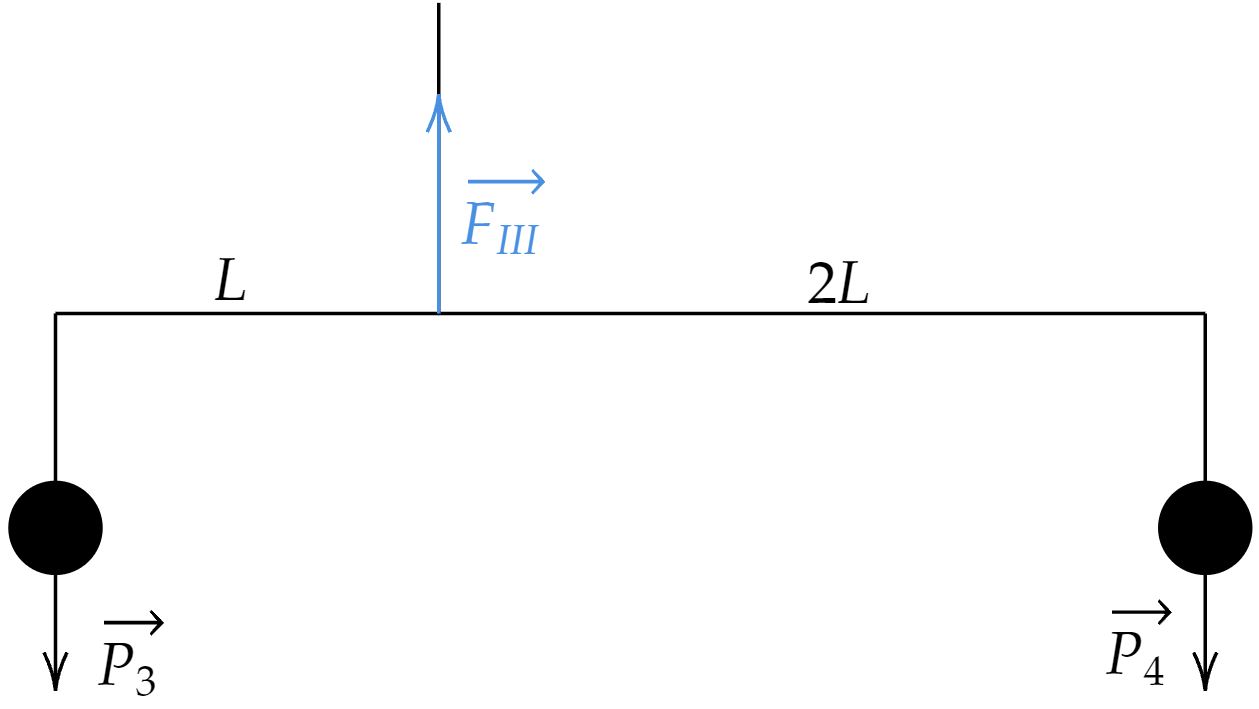 Com isso, é possível começar analisando o momento das forças que atuam o ponto da força $\vec{F}_{III}$, veja:\begin{matrix} P_3 \cdot L = P_4 \cdot 2L &\Rightarrow&
P_3 = 2 P_4
\end{matrix}Por outro lado, pensando no equilíbrio das forças: \begin{matrix}
F_{III} = P_3 + P_4 &\Rightarrow& \boxed{F_{III} =3 P_4}
\end{matrix}Agora, pensando no sistema acima deste, têm-se:
Com isso, é possível começar analisando o momento das forças que atuam o ponto da força $\vec{F}_{III}$, veja:\begin{matrix} P_3 \cdot L = P_4 \cdot 2L &\Rightarrow&
P_3 = 2 P_4
\end{matrix}Por outro lado, pensando no equilíbrio das forças: \begin{matrix}
F_{III} = P_3 + P_4 &\Rightarrow& \boxed{F_{III} =3 P_4}
\end{matrix}Agora, pensando no sistema acima deste, têm-se:
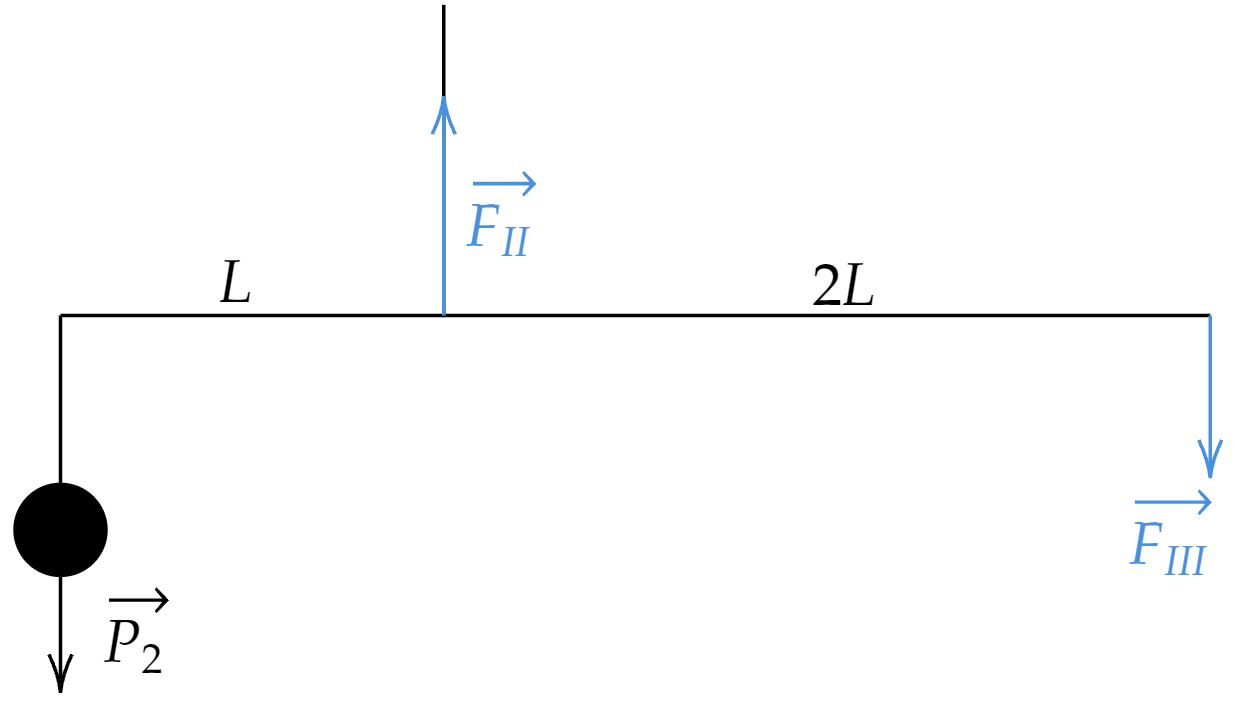 Analogamente, a partir da análise do momento das forças em relação ao ponto de atuação da força $\vec{F}_{II}$:\begin{matrix} P_2 \cdot L = F_{III} \cdot 2L &\Rightarrow&
P_2 = 6 P_4
\end{matrix}Pensando no equilíbrio das forças: \begin{matrix}
F_{II} = P_2 + F_{III} &\Rightarrow& \boxed{F_{II} =9 P_4}
\end{matrix}Novamente, num raciocínio análogo:
Analogamente, a partir da análise do momento das forças em relação ao ponto de atuação da força $\vec{F}_{II}$:\begin{matrix} P_2 \cdot L = F_{III} \cdot 2L &\Rightarrow&
P_2 = 6 P_4
\end{matrix}Pensando no equilíbrio das forças: \begin{matrix}
F_{II} = P_2 + F_{III} &\Rightarrow& \boxed{F_{II} =9 P_4}
\end{matrix}Novamente, num raciocínio análogo:
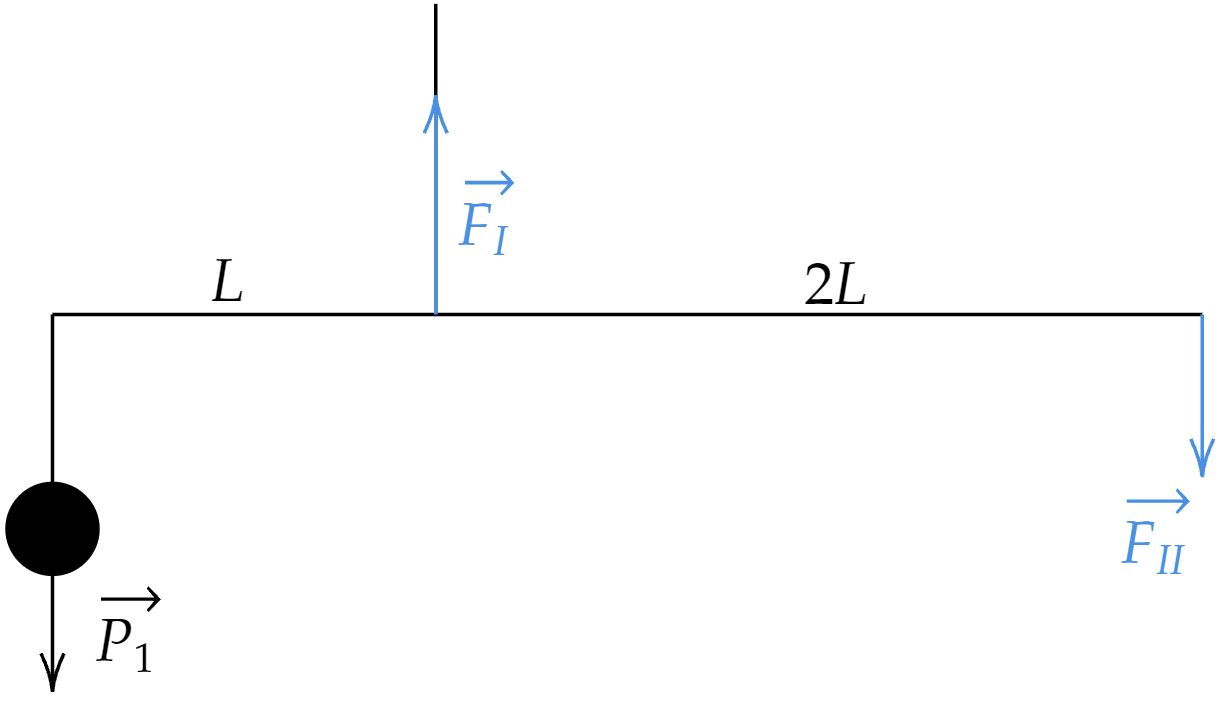 Por fim, analisando o momento das forças em relação ao ponto que atua a força $\vec{F}_{I}$:\begin{matrix} P_1 \cdot L = F_{II} \cdot 2L &\Rightarrow&
P_1 = 18 P_4 &\Rightarrow&m_1 =18m_4 &\therefore& \boxed{m_1 =0,18 \ \pu{kg}} &\tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}
Por fim, analisando o momento das forças em relação ao ponto que atua a força $\vec{F}_{I}$:\begin{matrix} P_1 \cdot L = F_{II} \cdot 2L &\Rightarrow&
P_1 = 18 P_4 &\Rightarrow&m_1 =18m_4 &\therefore& \boxed{m_1 =0,18 \ \pu{kg}} &\tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}

Ampliar Imagem

Ampliar Imagem

Ampliar Imagem

