A priori, podemos pensar na variação aparente da gravidade a partir da rotação da terra. No caso, esboçando uma situação arbitrária, isto é, em que um corpo esteja em uma posição qualquer, temos: 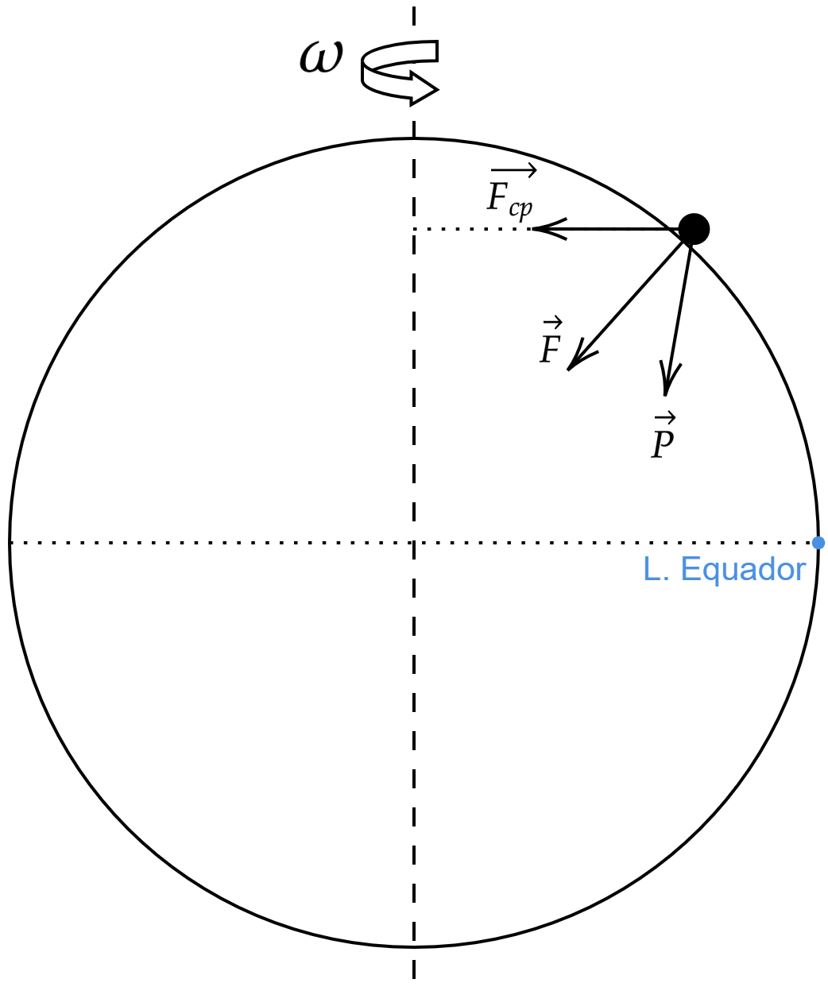Observe que $\vec{F}_{cp}$ é a componente centrípeta, assim como $\vec{P}$ representa o peso aparente e, $\vec{F}$ a força de atração gravitacional. Nesse contexto, pode-se equacionar: $$ \vec{F} = \vec{F}_{cp} + \vec{P}$$Atente que, quando o corpo estiver na linha do Equador, todos os vetores terão mesma direção e sentido, sendo possível escrever:$$ {F} = {F}_{cp} + {P}$$Para que o peso de uma pessoa seja nulo, certamente devemos ter $P$ sendo nulo, ou seja:\begin{matrix} F = F_{cp} &\Rightarrow& mg = m\omega^2 R &\therefore& \omega = \sqrt{\dfrac{g}{R}} \end{matrix}Atente que o $g$ é o módulo da aceleração gravitacional nos polos. Nesse sentido, já conseguirmos comparar a velocidade de rotação da terra $\omega_T$ com a necessária para anular o peso:\begin{matrix} \omega = \sqrt{\dfrac{9,8}{6,38 \cdot 10^6}} \ \pu{s^-1} &,& \omega_T = \dfrac{2\pi}{24 } \ \pu{h^-1} = \dfrac{2\pi}{24\cdot 60 \cdot 60} \ \pu{s^-1} \end{matrix}Continuando,\begin{matrix} \dfrac{\omega}{\omega_T} = \dfrac{\sqrt{\dfrac{9,8}{6,38 \cdot 10^6}}}{\dfrac{2\pi}{24\cdot 60 \cdot 60}} \approx 17 & \tiny{\blacksquare} \end{matrix} \begin{matrix}Letra \ (E) \end{matrix}