A priori, sabemos, segundo enunciado, a frequência que as faíscas são geradas, o que nos permite descobrir o intervalo de tempo entre as faíscas, no caso, $10^{-6} \ \pu{s}$. Nesse intervalo, o espelho está girando em torno de seu centro de curvatura, assim, podemos encontrar a partir de sua velocidade o comprimento percorrido pelo espelho em $10^{-6} \ s$, e por conseguinte, o intervalo entre duas faixas: \begin{matrix} V = \omega R = 2\pi f \cdot R = {\dfrac{\Delta S}{\Delta T}} &\Rightarrow& \Delta S = (2\pi \cdot 500) \cdot 1 \cdot 10^{-6} = \pi \cdot 10^{-6} \ \pu{m} &\Rightarrow& \fbox{$\Delta S = \pi \ \pu{mm}$} \end{matrix}No esboço abaixo, temos a situação descrita, veja que por pura geometria, o comprimento percorrido pelo espelho é metade do intervalo entre duas faixas luminosas. Isto é facilmente constado em vista do comprimento do espelho ao centro ser metade do comprimento do centro ao anteparo, isto é, o raio de uma circunferência é o dobro da outra. 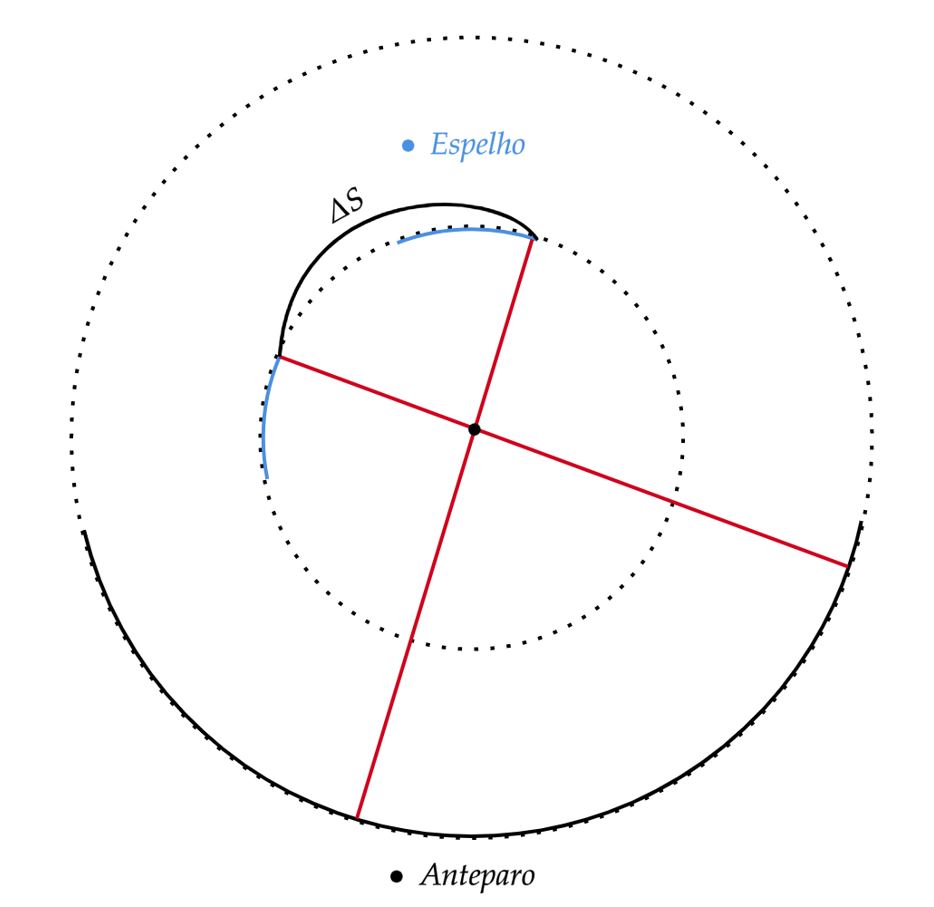Portanto, podemos escrever que, o comprimento do intervalo entre duas faixas $(x)$, será: \begin{matrix} x = 2 \ \Delta S &\Rightarrow& \fbox{$x \approx 6,3 \ \pu{mm} $} \end{matrix} \begin{matrix} Letra \ (B) \end{matrix}