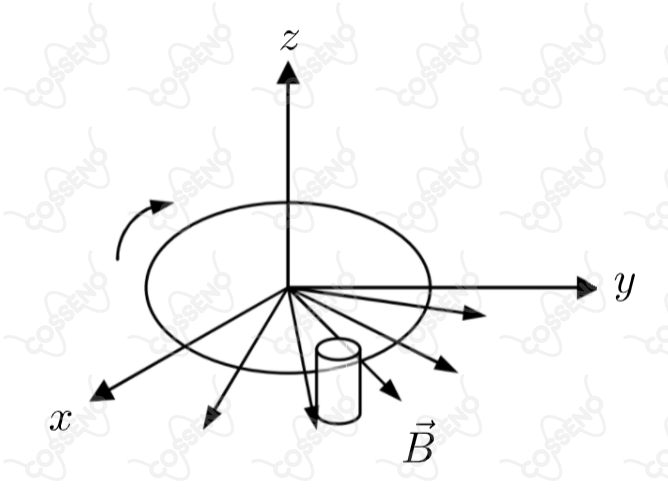
Um condutor reto, de de comprimento, é colocado paralelo ao eixo e gira com uma frequência de revoluções por minuto, descrevendo um círculo de diâmetro de no plano , como mostra a figura. Este condutor está imerso num campo magnético radial de módulo igual a . A tensão induzida nos terminais do condutor é de:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A priori, nota-se que o condutor irá se mover a todo momento com uma velocidade perpendicular ao campo magnético, isto é, os elétrons livres apresentarão uma força magnética paralela ao eixo $z$, com sentido para baixo. Nesse movimento dos elétrons, o condutor ficará polarizado, constata-se assim um campo elétrico, este que irá produzir uma força elétrica contrária a força magnética. Desse modo, o campo elétrico irá aumentar sua intensidade até as forças se igualarem, assim, têm-se a expressão: \begin{matrix} F_M = F_e &\Rightarrow& B\cdot |e|\cdot v = E\cdot |e|&\therefore& B\cdot v = E
\end{matrix}A partir do campo elétrico $E$, podemos definir a tensão induzida no condutor, veja: \begin{matrix} \Delta V = E \cdot l &,& l : \text{Comprimento do condutor}
\end{matrix}Assim, \begin{matrix} \Delta V = B\cdot v\cdot l
\end{matrix}Por $v$, entende-se como a velocidade tangencial do condutor, esta que podemos encontrar a partir dos dados fornecidos pelo enunciado, atente que a frequência deve ser passada para segundos:\begin{matrix} v = \omega \cdot R = 2\pi f \cdot R &,& R : \text{Raio do círculo}
\end{matrix}Continuando,\begin{matrix} \Delta V = B\cdot (2\pi f \cdot R )\cdot l \approx 0,5\cdot \left(2 \cdot 3,14 \cdot {\dfrac{50}{3}} \cdot 40\cdot 10^{-2} \right)\cdot 1\cdot 10^{-2}
\end{matrix}Portanto, \begin{matrix} \Delta V \approx 0,105 \ \pu{V} & \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}

