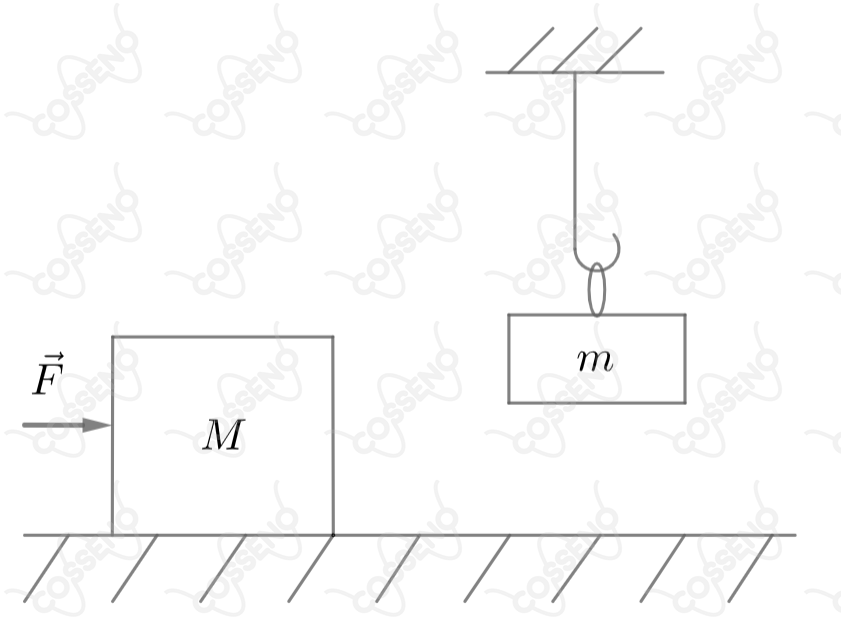
Um bloco de massa desliza por uma superfície horizontal sem atrito, empurrado por uma força , como mostra a figura abaixo. Esse bloco colide com outro de massa em repouso, suspenso por uma argola de massa desprezível e também em atrito. Após a colisão, o movimento é mantido pela mesma força , tal que o bloco de massa permanece unido ao de massa em equilíbrio vertical, devido ao coeficiente de atrito estático existente entre os dois blocos. Considerando a aceleração da gravidade e a velocidade instantânea do primeiro bloco logo antes da colisão, a potência requerida para mover o conjunto, logo após a colisão, tal que o bloco de massa não deslize sobre o outro, é dada pela relação:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Em uma colisão inelástica não podemos conservar a energia mecânica, então em primeira análise recorremos à conservação do momento linear (quantidade de movimento):$$Q_{\text{inicial}}=Q_{\text{final}}$$$$M\cdot V_0 = (M + m)\cdot V$$$$V=\frac{M}{M+m}V_0$$
Logo, em relação ao solo, o conjunto formado pelos blocos move-se com velocidade $V$ calculada acima. A figura do enunciado pode confundir um pouco, mas lendo o enunciado atentamente percebemos que após a colisão o bloco de massa $m$ ficará na face direita do bloco de massa $M$, estático em relação a ele devido à força de atrito que impede o deslizamento vertical do bloco de massa $m$. Para calcular a potência da força $F$, antes é necessário determinar $F$ em função dos dados do problema. Assim, analisando as forças presentes no sistema:$$\begin{cases}F-N=M\cdot a\quad(\text{Horizontal - Bloco }M)\\N=m\cdot a\qquad\quad\,(\text{Horizontal - Bloco }m)\\mg = F_{at}\qquad\quad\ \ \,(\text{Vertical - Bloco }m)\end{cases}$$Como $F_{at}=\mu_e\cdot N$, na terceira equação obtemos:$$N=\frac{mg}{\mu_e}$$Substituindo $N$ na segunda equação, obtemos:$$a=\frac{g}{\mu_e}$$Substituindo $N$ e $a$ na primeira equação, enfim determinamos $F$:$$F=\frac{(M+m)g}{\mu_e}$$Agora, para determinar a potência desempenhada pela força $F$:$$Pot=\frac{\text{Trabalho}}{\Delta t}=\frac{F\cdot\Delta s}{\Delta t}=F\cdot V$$$$Pot = \left(\frac{(M+m)g}{\mu_e}\right)\cdot\left(\frac{M}{M+m}V_0\right)$$$$\boxed{Pot=\frac{gMV_0}{\mu_e}}$$

