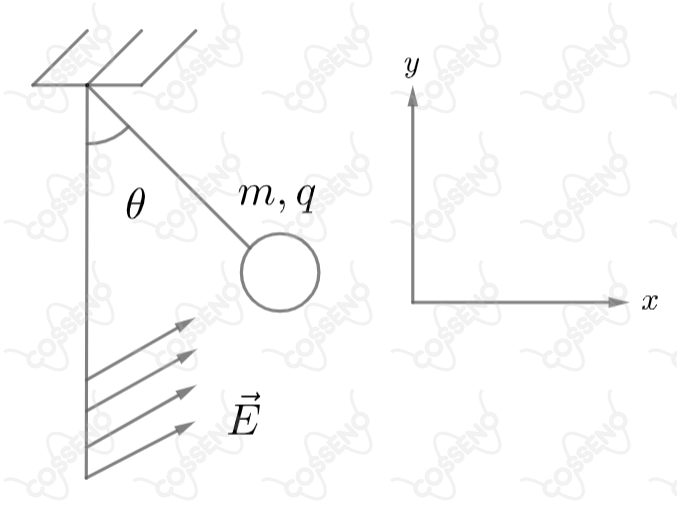
Uma esfera homogênea de carga e massa de está suspensa por um fio de massa desprezível em um campo elétrico cujas componentes e têm intensidades , respectivamente, como mostra a figura abaixo. Considerando que a esfera está em equilíbrio para qual é a força de tração no fio?
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A priori, da situação descrita, temos:
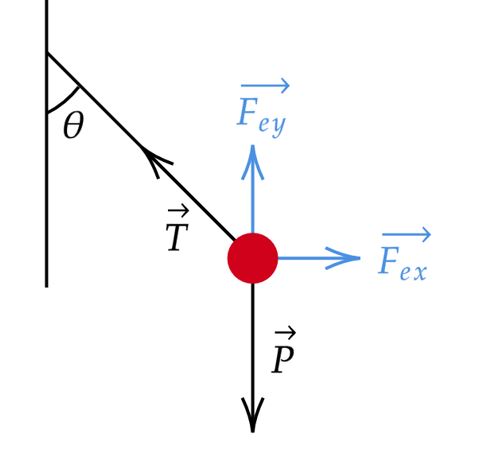 Decompondo a tração, encontramos duas equações, uma em cada eixo:
\begin{matrix} x: & T \cdot\cos{\theta} = F_{ex} &&,&& y :& T \cdot \sin{\theta} + F_{ey} = P \\ \\
x: & \dfrac{1}{2}T = E_x \cdot q &&\Rightarrow&& y :& E_x \cdot q \cdot \sqrt{3} + E_y \cdot q = mg
\end{matrix} Com isso, \begin{matrix} q = \dfrac{mg}{(E_x \sqrt{3} + E_y)} &\Rightarrow&
\dfrac{1}{2}T = E_x \cdot \dfrac{mg}{(E_x \sqrt{3} + E_y)}
&\therefore&\fbox{$T \approx 1,96 \cdot 10^{-3} \ N $}
\end{matrix} \begin{matrix} Letra \ (B)
\end{matrix}$\color{orangered}{Obs:}$ Lembre-se que a massa é em $\pu{kg}$.
Decompondo a tração, encontramos duas equações, uma em cada eixo:
\begin{matrix} x: & T \cdot\cos{\theta} = F_{ex} &&,&& y :& T \cdot \sin{\theta} + F_{ey} = P \\ \\
x: & \dfrac{1}{2}T = E_x \cdot q &&\Rightarrow&& y :& E_x \cdot q \cdot \sqrt{3} + E_y \cdot q = mg
\end{matrix} Com isso, \begin{matrix} q = \dfrac{mg}{(E_x \sqrt{3} + E_y)} &\Rightarrow&
\dfrac{1}{2}T = E_x \cdot \dfrac{mg}{(E_x \sqrt{3} + E_y)}
&\therefore&\fbox{$T \approx 1,96 \cdot 10^{-3} \ N $}
\end{matrix} \begin{matrix} Letra \ (B)
\end{matrix}$\color{orangered}{Obs:}$ Lembre-se que a massa é em $\pu{kg}$.

Ampliar Imagem
Decompondo a tração no fio, determina-se as duas relações abaixo:$$\begin{cases}T\sin \theta~=~qE_x\\T\cos \theta~=~mg-qE_y\end{cases} \implies \tg \theta~=~\dfrac{qE_x}{mg-qE_y}~=~\dfrac{E_x}{\frac{mg}{q}-E_y}~=~\sqrt{3~}$$Sabendo que $E_x=E_y\sqrt{3}$ , temos:$$E_x~=~\dfrac{mg\sqrt{3}}{q} - E_y\sqrt{3} \implies qE_x~=~\dfrac{mg\sqrt{3}}{2}~=~mg\sin \theta$$Assim, das relações iniciais, e considerando $g=9,8~\pu{m/s}^2$ :$$T\sin \theta~=~mg\sin \theta \implies T~=~mg \implies T~\cong~2\cdot 10^{-3}\cdot 9,8\implies \boxed{T~=~1,96\cdot 10^{-2}~\pu{N}}$$
$$\bf{Alternativa~(B)}$$


