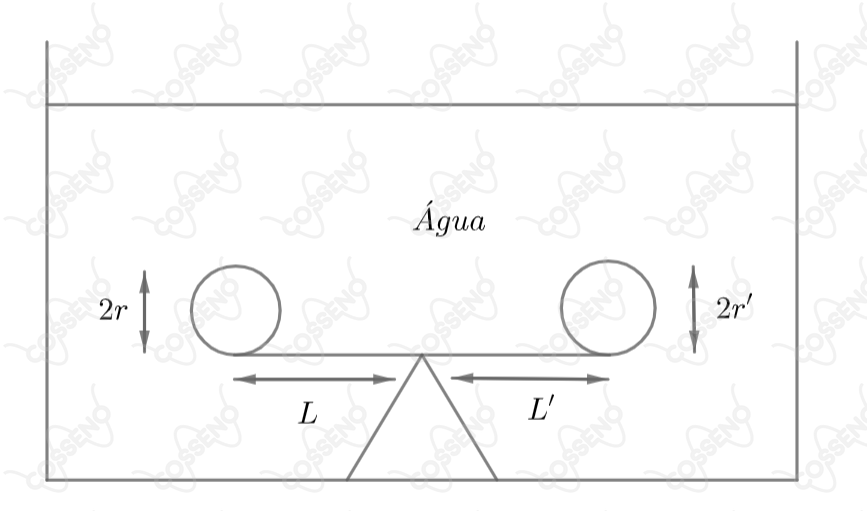
Duas esferas metálicas homogêneas de raios e e massas específicas de e , respectivamente, têm mesmo peso no vácuo. As esferas são colocadas nas extremidades de uma alavanca e o sistema todo mergulhado em água, como mostra a figura abaixo. A razão entre os dois braços de alavanca () para que haja equilíbrio é igual a:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A priori, repare nas forças que as esferas aplicam na barra, esta é a diferença entre o peso e o empuxo que atua em cada uma. No caso, podemos equacionar:\begin{matrix}F = P - E &,& F' = P - E'
\end{matrix}Observe que podemos relacionar o empuxo e o peso:\begin{matrix}\begin{cases}
P = \rho \cdot V \cdot g \\
E = \mu \cdot V \cdot g
\end{cases} &\Rightarrow& E = P \cdot \dfrac{\mu}{\rho} &,&
\begin{cases}
P = \rho' \cdot V' \cdot g \\
E' = \mu \cdot V' \cdot g
\end{cases} &\Rightarrow& E' = P \cdot \dfrac{\mu}{\rho'}
\end{matrix}Com isso,\begin{matrix} F = P \left( 1 - \dfrac{\mu}{\rho} \right) &,&F' = P \left( 1 - \dfrac{\mu}{\rho'} \right)
\end{matrix}Agora, pode-se analisar o momento das forças em relação ao ponto de suporte da alavanca, em que:\begin{matrix}
F \cdot L = F' \cdot L' &\Rightarrow& \dfrac{L}{L'} = \dfrac{\left( 1 - \dfrac{\mu}{\rho'} \right) }{\left( 1 - \dfrac{\mu}{\rho} \right) } = \dfrac{\left( 1 - \dfrac{1}{10} \right) }{\left( 1 - \dfrac{1}{5} \right) } &\therefore& \dfrac{L}{L'} = \dfrac{9}{8} & \tiny{\blacksquare}
\end{matrix}
\begin{matrix}Letra \ (C)
\end{matrix}

