Sejam , , e subconjuntos não vazios de . Considere as afirmações:
I - Se , então e .
II - Se , então .
III - Se , então .
Então:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$• \ \text{Afirmativa I:}$ $\color{#3368b8}{\text{Verdadeira}}$\begin{matrix}
(E \times G) \subset (F \times H) &\Rightarrow& \forall \ (a,b) \in (E \times G) \ \exists \ (a,b) \in (F \times H)
\end{matrix}Então, \begin{matrix} a \in E &\wedge& b \in G &\Leftrightarrow& a \in F &\wedge& b \in H
\end{matrix}Portanto,\begin{matrix} E \subset F &\wedge& G \subset H
\end{matrix}Graficamente,
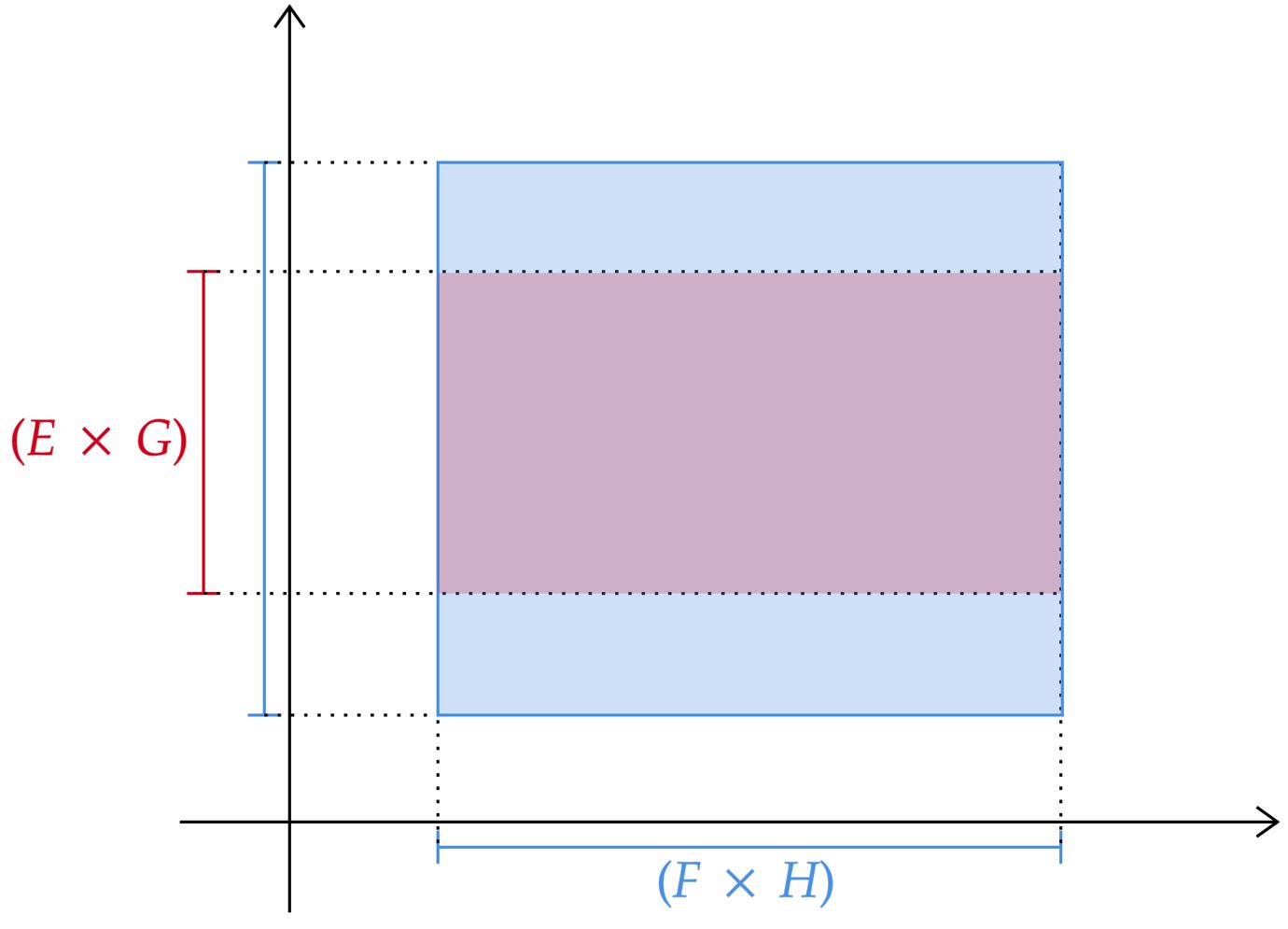 $• \ \text{Afirmativa II:}$ $\color{#3368b8}{\text{Verdadeira}}$ \begin{matrix} (E \times G) =X &\wedge& (F \times H) =Y &|& X \subset Y &\Rightarrow& X \cup Y = Y
\end{matrix}$• \ \text{Afirmativa III:}$ $\color{#3368b8}{\text{Verdadeira}}$ \begin{matrix} (E \times G) =X &\wedge& (F \times H) =Y &|& X \cup Y = Y &\Rightarrow& X \subset Y
\end{matrix}\begin{matrix}Letra \ (E)
\end{matrix}
$• \ \text{Afirmativa II:}$ $\color{#3368b8}{\text{Verdadeira}}$ \begin{matrix} (E \times G) =X &\wedge& (F \times H) =Y &|& X \subset Y &\Rightarrow& X \cup Y = Y
\end{matrix}$• \ \text{Afirmativa III:}$ $\color{#3368b8}{\text{Verdadeira}}$ \begin{matrix} (E \times G) =X &\wedge& (F \times H) =Y &|& X \cup Y = Y &\Rightarrow& X \subset Y
\end{matrix}\begin{matrix}Letra \ (E)
\end{matrix}

Ampliar Imagem

