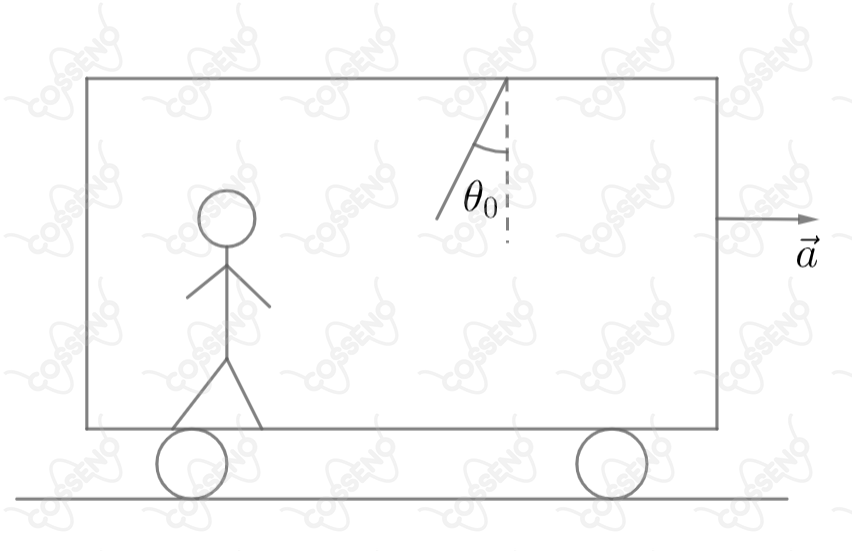
No inicio do século, Albert Einstein propôs que forças inerciais, como aquelas que aparecem em referenciais acelerados, sejam equivalentes às forças gravitacionais. Considere um pêndulo de comprimento suspenso no teto de um vagão de trem em movimento retilíneo com aceleração constante de módulo , como mostra a figura. Em relação a um observador no trem, o período de pequenas oscilações do pêndulo ao redor da sua posição de equilíbrio é:
O período de pequenas oscilações de um pêndulo pode ser expresso como:\begin{matrix}T = 2\pi \sqrt{\dfrac{L}{g_p}} &,& g_p: \text{campo gravitacional resultante no pêndulo}
\end{matrix}Observe que, como o vagão se desloca para direita com uma aceleração $\vec{a}$, o pêndulo deve "sentir" uma aceleração fictícia $-\vec{a}$. No caso, têm-se:
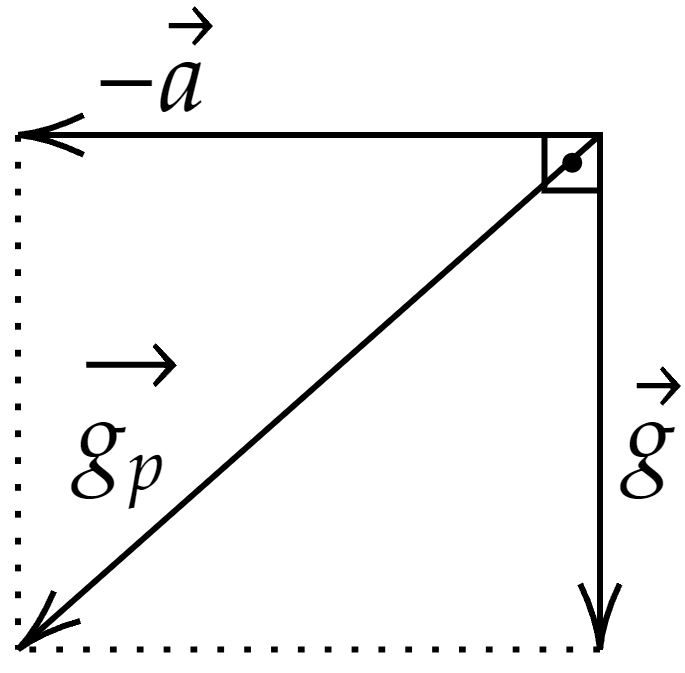Aplicando o teorema de Pitágoras, constatamos:\begin{matrix} g^2_p = g^2 + a^2 &\Rightarrow&g_p = \sqrt{ g^2 + a^2 } &\therefore& T = 2\pi \sqrt{\dfrac{L}{\sqrt{ g^2 + a^2 } }} &\tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}
Ampliar Imagem
