Um bloco maciço requer uma potência para ser empurrado, com uma velocidade constante, para subir uma rampa inclinada de um ângulo em relação à horizontal. O mesmo bloco requer uma potência quando empurrado com a mesma velocidade em uma região plana de mesmo coeficiente de atrito. Supondo que a única fonte de dissipação seja o atrito entre o bloco e a superfície, conclui-se que o coeficiente de atrito entre o bloco e a superfície é:
Primeiramente, podemos pensar na potência, esta que pode ser escrita como:\begin{matrix} Pot = F \cdot v &\Rightarrow& P = F_1 \cdot v &,& Q = F_2 \cdot v &\therefore& \dfrac{P}{Q} = \dfrac{F_1}{F_2} & (1)
\end{matrix}Nesse contexto, é possível esboçar cada situação, vejamos:
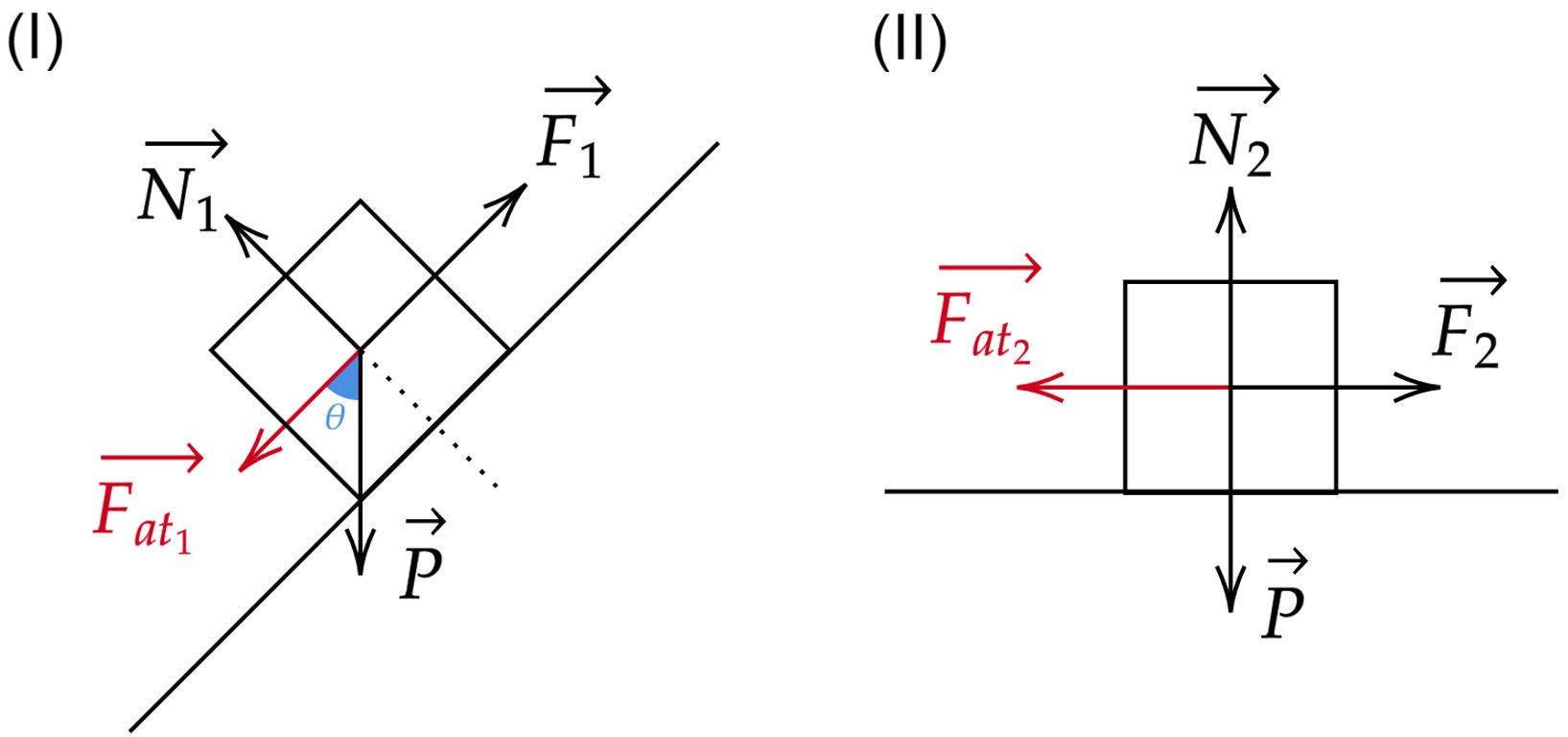Analisando as forças que atuam na situação $\text{(I)}$, têm-se:\begin{matrix}\begin{cases} N_1 &=& P \cos{\theta} \\ F_1 &=& F_{at_{1}} + P \sin{\theta}
\end{cases} &,&F_{at_{1}} = \mu N_1 &\Rightarrow& F_1 = P(\sin{\theta} + \mu \cos{\theta}) & (2)
\end{matrix}Já sobre as forças que atuam na situação $\text{(II)}$:\begin{matrix}\begin{cases} N_2 &=& P \\ F_2 &=& F_{at_{2}}
\end{cases} &,&F_{at_{2}} = \mu N_2 &\Rightarrow& F_2 = \mu P & (3)
\end{matrix}Substituindo $(2)$ e $(3)$ em $(1)$, constatamos:\begin{matrix} \dfrac{P}{Q} = \dfrac{\sin{\theta} + \mu \cos{\theta}}{\mu} &\Rightarrow& \mu P = Q\sin{\theta} + \mu Q \cos{\theta} &\therefore&\mu = \dfrac{Q \sin{\theta}}{P - Q \cos{\theta}} & \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (E)
\end{matrix}
Ampliar Imagem
