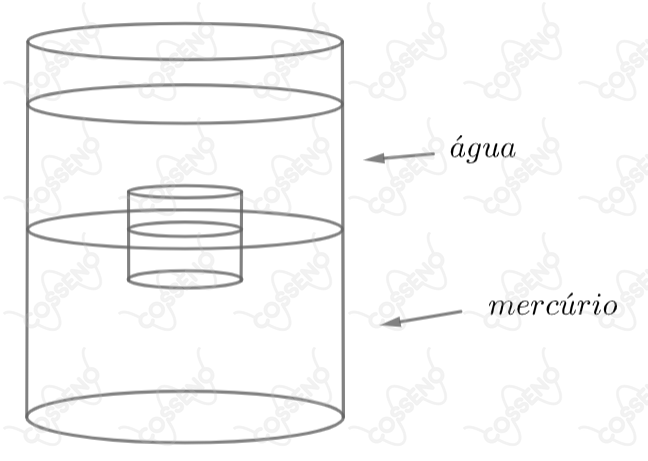
Um cilindro maciço flutua verticalmente, com estabilidade, com uma fração do seu volume submerso em mercúrio, de massa especifica . Coloca-se água suficiente (de massa especifica ) por cima do mercúrio, para cobrir totalmente o cilindro, e observa-se que o cilindro continue em contato com o mercúrio após a adição da água. Conclui-se que o mínimo valor da fração originalmente submersa no mercúrio é:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Assumindo que o cilindro apresente um volume $V$, podemos supor que na situação inicial o volume submerso é $V_1$. Nesse contexto, no equilíbrio temos a relação entre o empuxo e a força peso, tal que:\begin{matrix}
E = P &\Rightarrow& D \cdot V_1 \cdot g =m g &,& m = \rho \cdot V &\therefore& \dfrac{V_1}{V} = \dfrac{\rho}{D} = f
\end{matrix}Já na segunda situação, vamos admitir que exista um volume $V_2$ submerso no mercúrio e um volume $V_3$ submerso na água. Certamente, $V_2 + V_3 = V$, em que diferentes empuxos atuam sobre o cilindro, tal que:\begin{matrix} E_2 + E_3 = mg &\Rightarrow&
D \cdot V_2 \cdot g + d \cdot V_3 \cdot g = \rho \cdot V \cdot g
\end{matrix}Veja que para haver contato com o mercúrio, $V \ge 0$, em que o limite é a igualdade. Desse modo, continuando:\begin{matrix}D \cdot V_2 + d \cdot (V-V_2) = \rho \cdot V &\Rightarrow&
V_2 + \dfrac{d}{D}(V-V_2) = f \cdot V &\Rightarrow&V_2 \left( 1 - \dfrac{d}{D} \right) = V\left( f - \dfrac{d}{D} \right)
\end{matrix}Com isso,\begin{matrix} V_2 = \dfrac{V\left( f - \dfrac{d}{D} \right)
}{ \left( 1 - \dfrac{d}{D} \right)} \ge 0 &\therefore& f \ge \dfrac{d}{D} &\tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (C)
\end{matrix}

