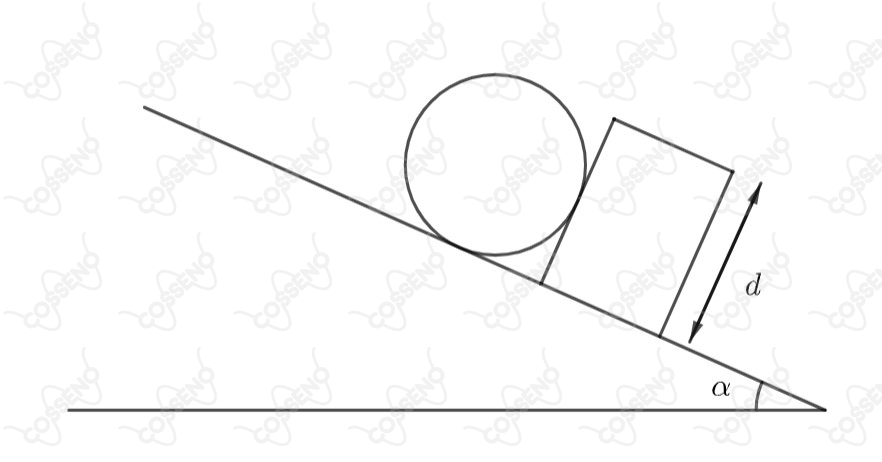
Considere um bloco cúbico de lado e massa em repouso sobre um plano inclinado de ângulo , que impede o movimento de um cilindro de diâmetro e massa idêntica à do bloco, como mostra a figura. Suponha que o coeficiente de atrito estático entre o bloco e o plano seja suficientemente grande para que o bloco não deslize pelo plano e que o coeficiente de atrito estático entre o cilindro e o bloco seja desprezível. O valor máximo do ângulo do plano inclinado, para que a base do bloco permaneça em contato com o plano, é tal que:
Analisando as forças que atuam em cada corpo, têm-se:
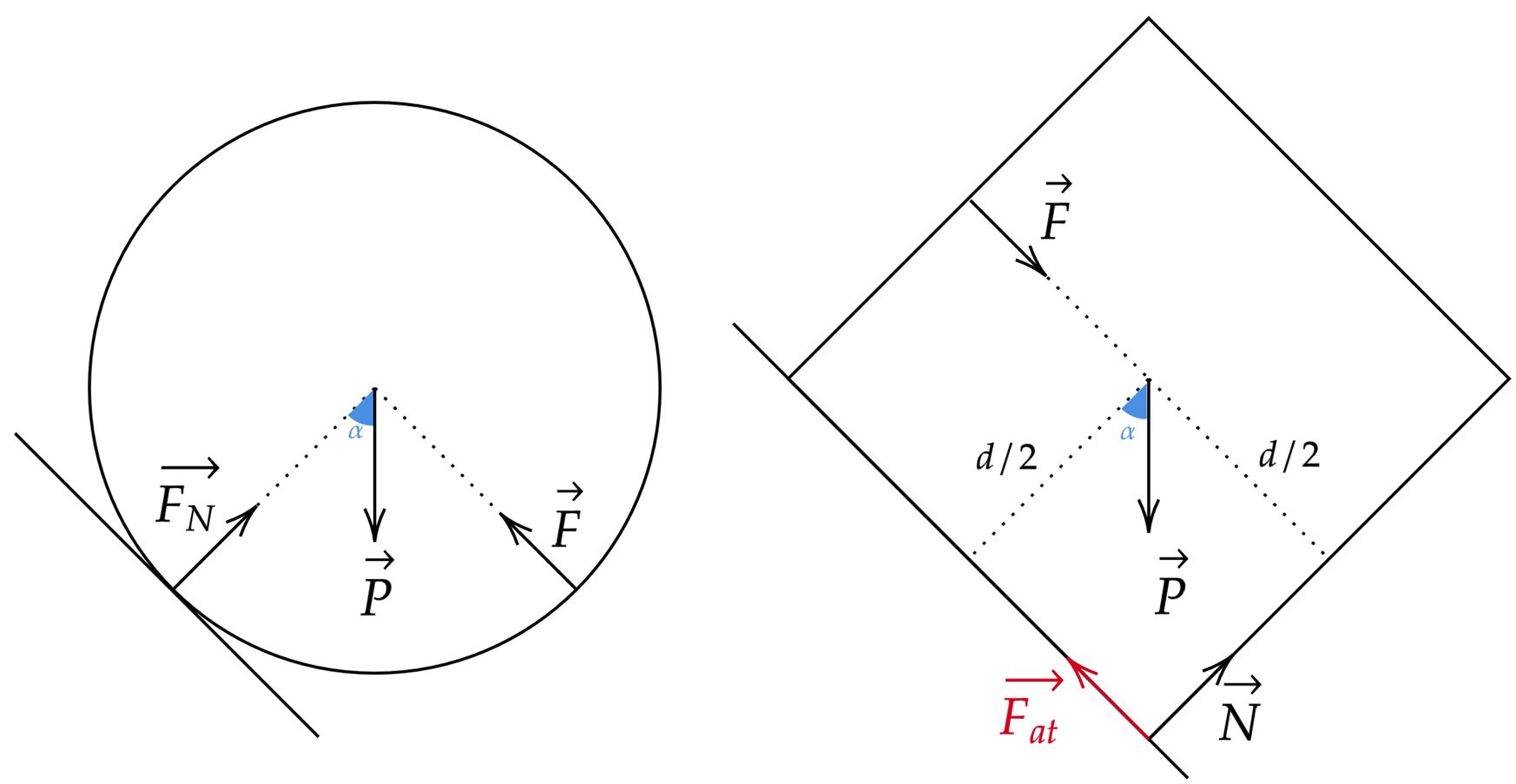Primeiramente, observe que na iminência de tombar, toda a reação da superfície se concentrará no extremo do bloco, como mostra o esboço. Nesse contexto, podemos partir da análise das foças do cilindro, este que também deve estar em equilíbrio, tal que:\begin{matrix} F = P\sin{\alpha} & (1)
\end{matrix}Agora, analisando o cubo, é possível se analisar o momento das forças em relação ao centro de gravidade, em que:\begin{matrix} F_{at} \cdot \dfrac{d}{2} = N \cdot \dfrac{d}{2} &,& F_{at} = \mu N &\therefore& \mu = 1
\end{matrix}Já pelo equilíbrio de forças:\begin{matrix}N = P\cos{\alpha} &,& F + P\sin{\alpha} = F_{at} &\overset{(1)}{\Rightarrow}& 2P\sin{\alpha} = \mu P\cos{\alpha} &\therefore& \cot{\alpha} = 2
& \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (E)
\end{matrix}
Ampliar Imagem
