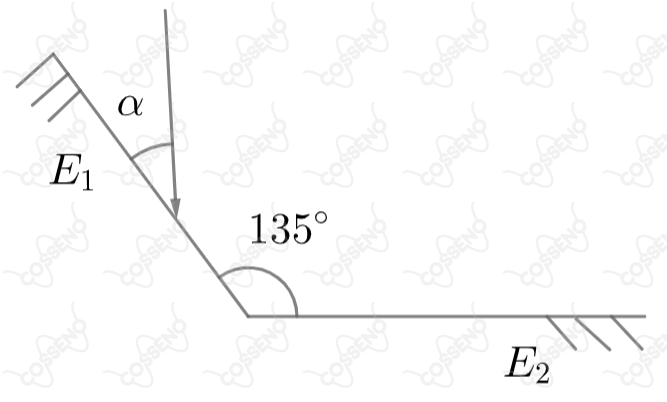
Considere a figura abaixo onde e são dois espelhos planos que formam um ângulo de entre si. Um raio luminoso incide com um ângulo em e outro (não mostrado) emerge de . Para , conclui-se que:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A priori, vamos esboçar uma situação genérica para o paralelismo entre os raios, assim, temos:
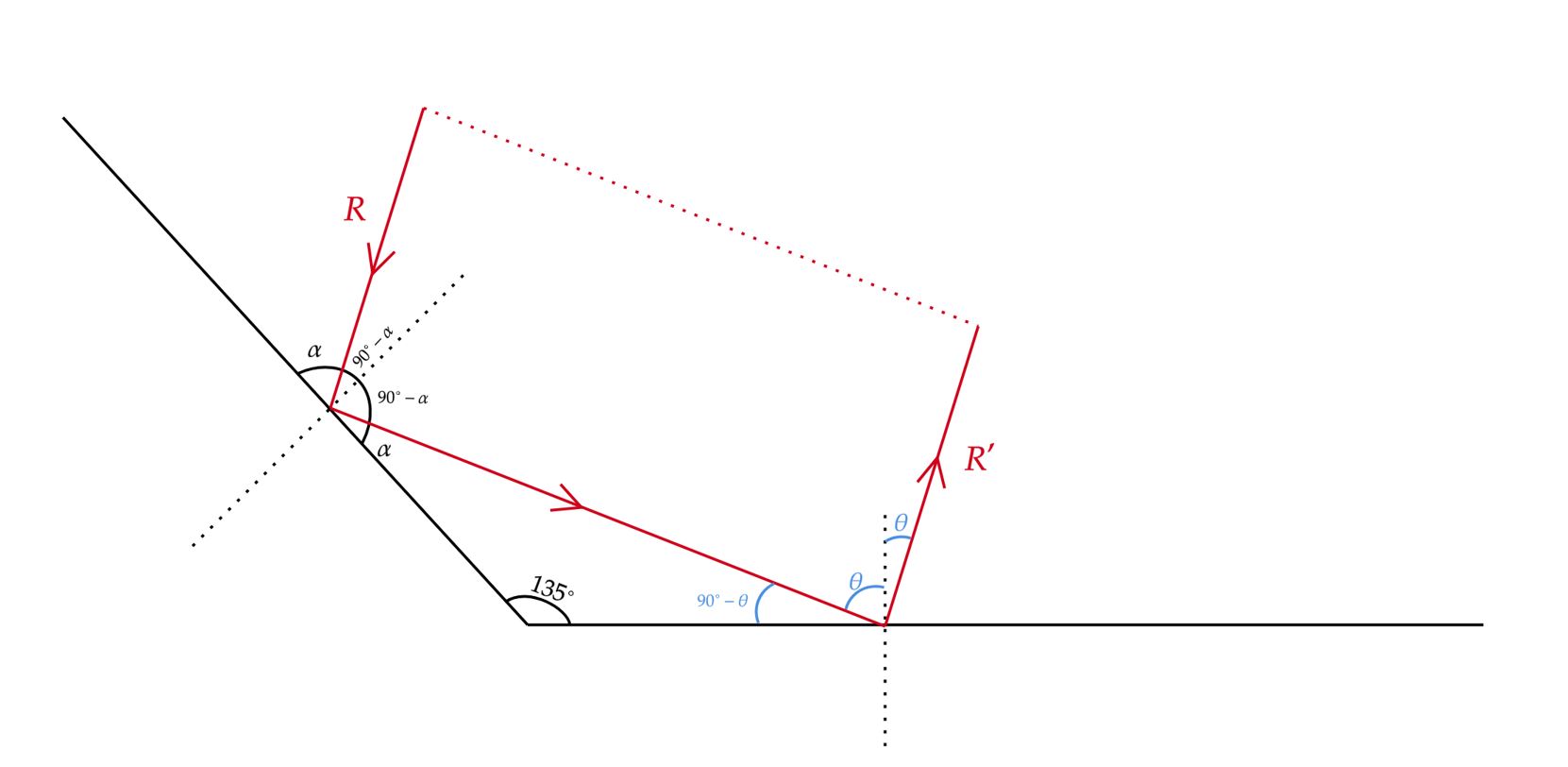 Perceba que, como $R$ e $R^{'}$ serão paralelos, teremos um paralelogramo, o qual podemos tirar uma equação a partir da soma de seus ângulos. Por outro lado, veja que também temos um triângulo obtuso, com ângulo de $135^{\circ}$, assim, têm-se:
\begin{matrix} 135^{\circ} + \alpha + (90^{\circ} - \theta) = 180^{\circ} &\Rightarrow& \fbox{$\theta = \alpha + 45^{\circ}$}
\end{matrix}
Agora, com conhecimento das propriedades do paralelogramo, podemos escrever:
\begin{matrix} 2.(90^{\circ} - \alpha) + 2.(2 \theta) = 360^{\circ} &\Rightarrow& \fbox{$\theta = 45^{\circ}$} &\Rightarrow& \fbox{$\alpha= 0^{\circ}$}
\end{matrix}Vide enunciado, $0^{\circ} <\alpha< 45^{\circ}$, o que nos leva a dizer que $\text{$R^{'}$ nunca é paralelo a $R$}$.
\begin{matrix} Letra \ (C)
\end{matrix}
Perceba que, como $R$ e $R^{'}$ serão paralelos, teremos um paralelogramo, o qual podemos tirar uma equação a partir da soma de seus ângulos. Por outro lado, veja que também temos um triângulo obtuso, com ângulo de $135^{\circ}$, assim, têm-se:
\begin{matrix} 135^{\circ} + \alpha + (90^{\circ} - \theta) = 180^{\circ} &\Rightarrow& \fbox{$\theta = \alpha + 45^{\circ}$}
\end{matrix}
Agora, com conhecimento das propriedades do paralelogramo, podemos escrever:
\begin{matrix} 2.(90^{\circ} - \alpha) + 2.(2 \theta) = 360^{\circ} &\Rightarrow& \fbox{$\theta = 45^{\circ}$} &\Rightarrow& \fbox{$\alpha= 0^{\circ}$}
\end{matrix}Vide enunciado, $0^{\circ} <\alpha< 45^{\circ}$, o que nos leva a dizer que $\text{$R^{'}$ nunca é paralelo a $R$}$.
\begin{matrix} Letra \ (C)
\end{matrix}

Ampliar Imagem

