Um diapasão de soa acima de um tubo de ressonância contendo um êmbolo móvel como mostrado na figura. A uma temperatura ambiente de , a primeira ressonância ocorre quando o êmbolo está a uma distância abaixo do topo do tubo. Dado que a velocidade do som no ar (em ) a uma temperatura (em ) é , conclui-se que a a posição do êmbolo para a primeira ressonância, relativa a sua posição a , é:
Na situação do enunciado, temos algo como dois tubos sonoros fechados em uma das extremidades , ambos em primeira ressonância (primeiro harmônico). Dessa forma, podemos supor:
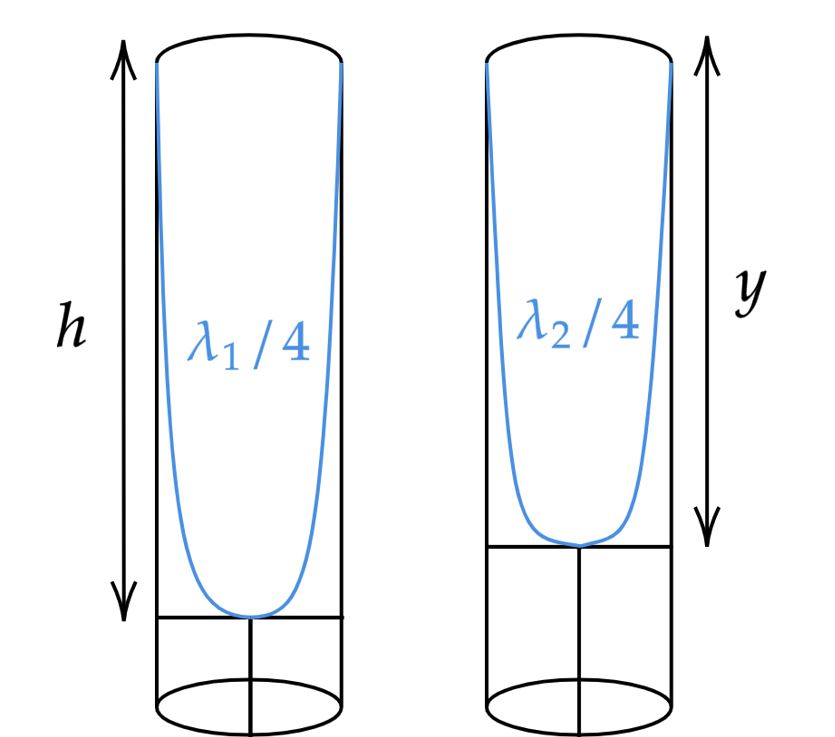\begin{matrix} h = {\dfrac{\lambda_1}{4} } &,& y = {\dfrac{\lambda_2}{4} }
\end{matrix}Sabido que, a frequência permanecerá constante nas duas situações, é possível escrever a partir da equação fundamental da ondulatória:
• $h$: \begin{matrix} v_h = \lambda_1\cdot f &\Rightarrow& 331,5 = 4h\cdot 440 &\therefore& h = {\dfrac{331,5}{4\cdot 440}}
\end{matrix}• $y$: \begin{matrix} v_y = \lambda_2\cdot f &\Rightarrow& 331,5 + 0,607\cdot 20 = 4y\cdot 440 &\therefore& y = {\dfrac{331,5 + 12,14}{4\cdot 440}}
\end{matrix}Continuando, \begin{matrix} h - y = -\dfrac{12,14}{4\cdot 440} &\therefore& h - y \approx -0,7 \ \pu{cm}
\end{matrix}$\color{orangered}{Obs:}$ O sinal negativo informa que a nossa suposição foi equivocada, o êmbolo não sobe, na verdade, ele desce $0,7 \ \pu{cm}$.\begin{matrix} Letra \ (C)
\end{matrix}
Ampliar Imagem
