Um 'bungee jumper' de de altura e de massa pula de uma ponte usando uma 'bungee cord', de de comprimento quando não alongada, constante elástica de e massa desprezível, amarrada aos seus pés. Na sua descida, a partir da superfície da ponte, a corda atinge a extensão máxima sem que ele toque nas rochas embaixo. Das opções abaixo, a menor distância entre a superfície da ponte e as rochas é:
Admitindo que o 'bungee jumper' apresenta seu centro de gravidade à meia altura, e que a corda é amarrada aos seus pés (como comumente é), podemos esboçar a seguinte situação:
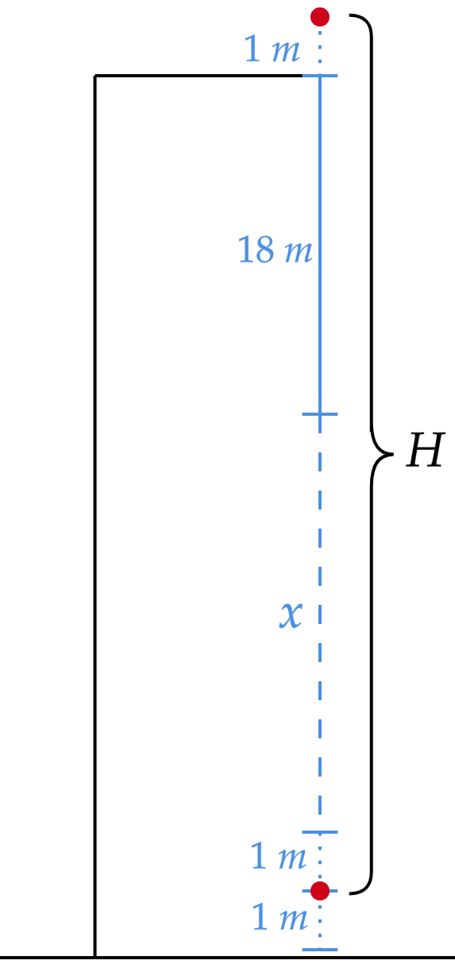Com isso, assumindo que não haja dissipação de energia, pode-se aplicar o teorema da energia cinética, em que tanto no caso inicial quanto final a velocidade é nula. Nesse sentido, não esqueça que a situação final é a maior extensão da corda, quando ocorre o repouso momentâneo do corpo, tal que:\begin{matrix}W_T = \Delta E_c &\Rightarrow& mgH - \dfrac{Kx^2}{2} = 0 &\Rightarrow& 100 \cdot 10 \cdot (1 + 18 +x +1) = 100 \cdot x^2
\end{matrix}Continuando,\begin{matrix} x^2 - 10x - 200 = 0 &\Rightarrow& (x-5)^2 = 225 &\therefore& \boxed{x = 20 \ \pu{m}}
\end{matrix}Analisando novamente a figura, nota-se que existem mais um metro de corpo do 'bungee jumper' até o solo. Portanto, a menor distância entre a superfície da ponte e as rochas, nesse caso, seria: $\boxed{41 \ \pu{m}}$\begin{matrix}Letra \ (D)
\end{matrix}
Ampliar Imagem
