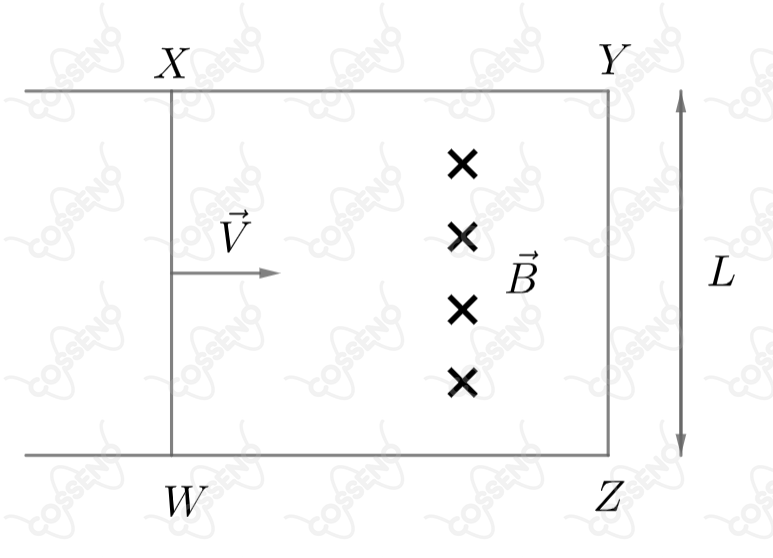
Uma haste de comprimento desloca-se com velocidade constante sobre dois trilhos paralelos separados por uma distância , na presença de um campo de indução magnética, uniforme e constante, de magnitude , perpendicular ao plano dos trilhos, direcionado para dentro do papel, como mostra a figura. Há uma haste fixada no término dos trilhos. As hastes e os trilhos são feitos de um fio condutor cuja resistência por unidade de comprimento é . A corrente na espira retangular :
CossenoGPT
Teste gratuitamente agora mesmo! 

Com conhecimento da $\text{Lei de Lenz}$, entende-se que essa variação do fluxo magnético acarretará numa corrente. Nesse viés, o sistema tende a repor o fluxo "perdido", isto é, a corrente em prol de criar um campo magnético entrando no papel, sendo assim o $\text{sentido da corrente horário}$.
Agora, acerca da intensidade da corrente, vale começar pela $\text{Lei de Faraday-Neumann}$, por ela, é sabido que a variação do fluxo magnético produz uma tensão induzida, esta representada pela expressão: \begin{matrix}|\varepsilon| = {{\dfrac{\phi}{\Delta t}}} = B\cdot v\cdot L
\end{matrix}Atente que, segundo enunciado, a velocidade da haste é constante, tal-qualmente o comprimento $L$, como o campo magnético. Com isso, têm-se uma tensão constante, a qual podemos analisar a partir da $\text{Primeira Lei de Ohm}$: \begin{matrix} \varepsilon = R\cdot i
\end{matrix}Veja que, conforme a haste se movimenta, a resistência diminui, pois o comprimento também diminui $\text{(Segunda Lei de Ohm)}$. Desse modo, $\text{a corrente aumenta tendendo a um valor limite}$, limite esse que ocorre no momento que a haste móvel chaga até a haste fixa. \begin{matrix} Letra \ (A)
\end{matrix}

