Decompondo a força $\vec{F}$ e analisando as forças que atuam no bloco, têm-se: 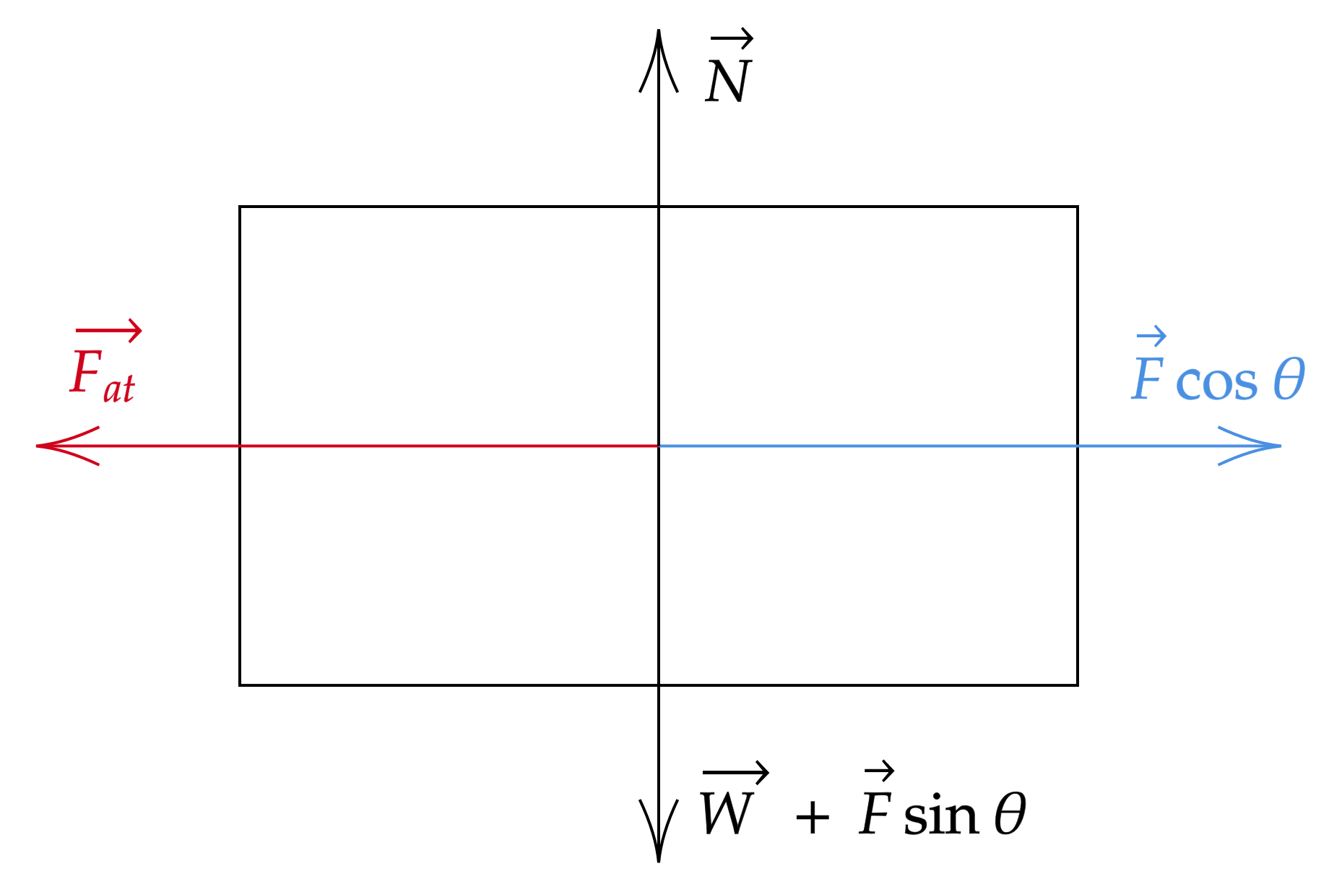Nesse contexto, podemos equacionar:\begin{matrix} \begin{cases} \ \ \ \ \ F \cos{\theta} &=& F_{at} \\ W+F \sin{\theta} &=& N \end{cases} &\Rightarrow& F \cos{\theta} \le \mu N &\Rightarrow& F \cos{\theta} \le \mu W + \mu F \sin{\theta} \end{matrix}Continuando,\begin{matrix} F \le \dfrac{\mu W}{\cos{\theta} - \mu \sin{\theta}} \cdot \color{#3368b8}{\dfrac{\cos{\theta}}{\cos{\theta}}} &\therefore& F \le \dfrac{\mu W \sec{\theta}}{1 -\mu \tan{\theta}} &\tiny{\blacksquare} \end{matrix}Atente que, na iminência do movimento, tem-se a igualdade da expressão.\begin{matrix} Letra \ (D) \end{matrix}

Decompondo a força $ F $ em suas componentes temos que a componente horizontal de $F$ é igual a $F \cos (\theta)$ e a sua componente vertical é igual $F \sin(\theta)$. Como o bloco não se move verticalmente , podemos escrever que : $N = F\sin(\theta) + W $ Perceba que na iminência do movimento podemos considerar que $F\cos(\theta)$ é praticamente igual ao atrito $fat$ , logo : $F\cos(\theta) = fat = F\cos(\theta) = \mu \cdot N $ $F\cos(\theta) = \mu \cdot ( F\sin(\theta) + W ) = F\cos(\theta) = \mu \cdot F\sin(\theta) + \mu \cdot W $ $\implies F(\cos(\theta) - \mu \cdot \sin(\theta)) = \mu \cdot W$ $ \implies F = \dfrac{\mu \cdot W}{\cos(\theta) - \mu \cdot \sin(\theta)} = F = \dfrac{\mu \cdot W}{(1 - \mu \cdot \tan(\theta))\cos(\theta)} = F = \dfrac{\mu W \sec(\theta)}{1 - \mu \tan(\theta)}$ $\textbf{Resposta : Letra D}$