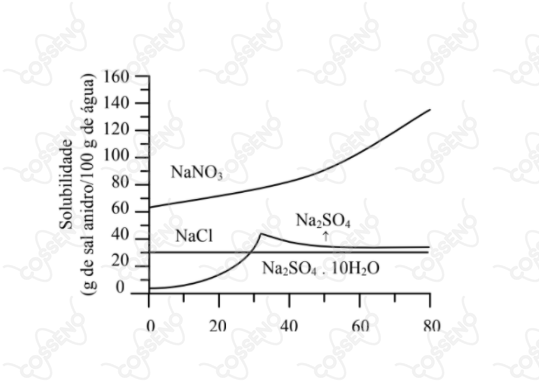
Considerando sistemas termodinamicamente estáveis, é errado afirmar que:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

$• \ \text{Alternativa (A):}$ $\color{royalblue}{\text{Verdadeira}}$
Olhar o gráfico.
$• \ \text{Alternativa (B):}$ $\color{orangered}{\text{Incorreta}}$
Na temperatura informada teremos uma solução satura, isto é, precipitado. Nessa perspectiva, teremos uma mistura bifásica, sendo uma das fases o ${NaNO_3}_{(s)}$, e a outra a solução de $NaNO_3$.
$• \ \text{Alternativa (C):}$ $\color{royalblue}{\text{Verdadeira}}$
Ao adicionar cloreto de sódio ao gelo, teremos a fusão do mesmo, formando uma mistura homogênea entre a água e o sal completamente dissolvido e dissociado. Nessa perspectiva, certamente teremos uma solução monofásica de $NaCl$ não saturada.
$• \ \text{Alternativa (D):}$ $\color{royalblue}{\text{Verdadeira}}$
A priori, segundo o gráfico, todo sal será dissolvido e dissociado, e conhecida sua dissociação, sabemos que há uma relação estequiométrica de $1:1:1$, assim: \begin{matrix} n_{(Na^+)} &=& {{\dfrac{1 \ \text{mol de} \ Na^+}{1 \ \text{mol de} \ NaCl}}} \ .\ {{\dfrac{1 \ \text{mol de} \ NaCl}{58,5 \ \text{g de} \ NaCl}}} \ .\ 6 \ \text{g de} \ NaCl &\therefore& n_{(Na^+)} \approx 0,1 \ mol
\end{matrix}Já o volume de água, \begin{matrix}V_{(H_2O)} &=& {{\dfrac{1 \ \text{ml de} \ H_2O}{1 \ \text{g de} \ H_2O}}} \ . \ 100 \ \text{g de} \ H_2O &\therefore& V_{(H_2O)} = 0,1 \ L
\end{matrix}Portanto,\begin{matrix} C_{(Na^+)} &\approx& {{\dfrac{0,1 \ \text{mol de} Na^+}{0,1 \ \text{L de} H_2O}} } &\therefore& C_{(Na^+)} \approx1 \ mol/L
\end{matrix}
$• \ \text{Alternativa (E):}$ $\color{royalblue}{\text{Verdadeira}}$
A priori, a situação não precisa de contas, pois é de se acreditar que o sal hidratado irá dissociar menos que o sal puro, assim a concentração de íons sódio na solução seria maior no sal puro. Entretanto, também é válido fazer as contas, veja:
\begin{matrix} Na_2SO_4: && n_{(Na^+)} &=& {{\dfrac{2.(23) \ \text{g de} \ Na^+}{142 \ \text{g de} \ Na_2SO_4}}} \ .\ 1 \ \text{g de} \ Na_2SO_4
&\therefore& n_{(Na^+)} = {{\dfrac{23}{72}}} \ mol \\ \\ Na_2SO_4 \cdot 10H_2O: && n_{(Na^+)} &=& {{\dfrac{2.(23) \ \text{g de} \ Na^+}{322 \ \text{g de} \ Na_2SO_4 \cdot 10H_2O}}} \ .\ 1 \ \text{g de} \ Na_2SO_4
&\therefore& n_{(Na^+)} = {{\dfrac{23}{161}}} \ mol
\end{matrix}Como o volume da solução será o mesmo em ambas as situações, não é difícil inferir que a alternativa está correta.
\begin{matrix}Letra \ (B)
\end{matrix}

