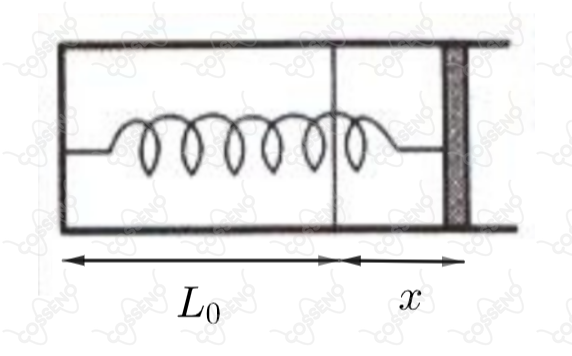
Um mol de gás perfeito está contido em um cilindro de secção fechado por um pistão móvel, ligado a uma mola de constante elástica . Inicialmente, o gás está na pressão atmosférica e temperatura , e o comprimento do trecho do cilindro ocupado pelo gás é , com a mola estando indeformada. O sistema gás-mola é aquecido e o pistão se desloca de uma distância . Denotando a constante de gás por , a nova temperatura do gás é
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Situação inicial: \begin{matrix} P_0V_0 = nRT_0 &\Rightarrow& P_0\cdot (S\cdot L_0) = RT_0
\end{matrix}Situação final: \begin{matrix} PV= nRT &\Rightarrow& P\cdot (L_0 + x)\cdot S = RT
\end{matrix}Pressão final: \begin{matrix} F_{gás} = F_{el} + F_{atm} &\Rightarrow& P\cdot S = k\cdot X + P_0\cdot S &\therefore& \fbox{$P = \dfrac{k\cdot X}{S} + P_0$}
\end{matrix}Substituindo nossos resultados: \begin{matrix} \left(\dfrac{k\cdot X}{S} + P_0 \right)\cdot (L_0 + x)\cdot S = RT
\end{matrix}Continuando, \begin{matrix} RT = (k\cdot X+ P_0\cdot S)\cdot (L_0 + x) \\ \\ RT = k\cdot X\cdot L_0 + k\cdot X^2 + P_0\cdot S\cdot L_0 +P_0\cdot S \cdot X \\ \\ \text{Obs:} \ \ {\fbox{$S\cdot L_0 = \dfrac{RT_0}{P_0}$}} \\ \\
RT = k\cdot X\cdot L_0 + k\cdot X^2 + P_0\cdot \dfrac{RT_0}{P_0} + P_0\cdot S\cdot X \\ \\ RT = X(k\cdot L_0 + k\cdot X + P_0\cdot S)+ RT_0 \\ \\ \fbox{$T = T_0 + \dfrac{X}{R}(k\cdot L_0 + k\cdot X + P_0\cdot S)$} \\ \\ Letra \ (E)
\end{matrix}

11:56 18/04/2023
Olá! O código LaTex está com erro. As equações não apareceram depois de "Continuando, ..."

