Conhecido o período do pêndulo simples para pequenas oscilações, têm-se:\begin{matrix} T = \sqrt{\dfrac{L}{g}} &\Rightarrow& T^2 \cdot g = L & (1) \end{matrix}Observe que o comprimento $L$ do pêndulo deve ser invariável, senão seríamos incapazes de fazer a análise. Nesse contexto, sabemos que a aceleração da gravidade deve mudar entre as regiões, observe abaixo uma representação extremamente desproporcional: 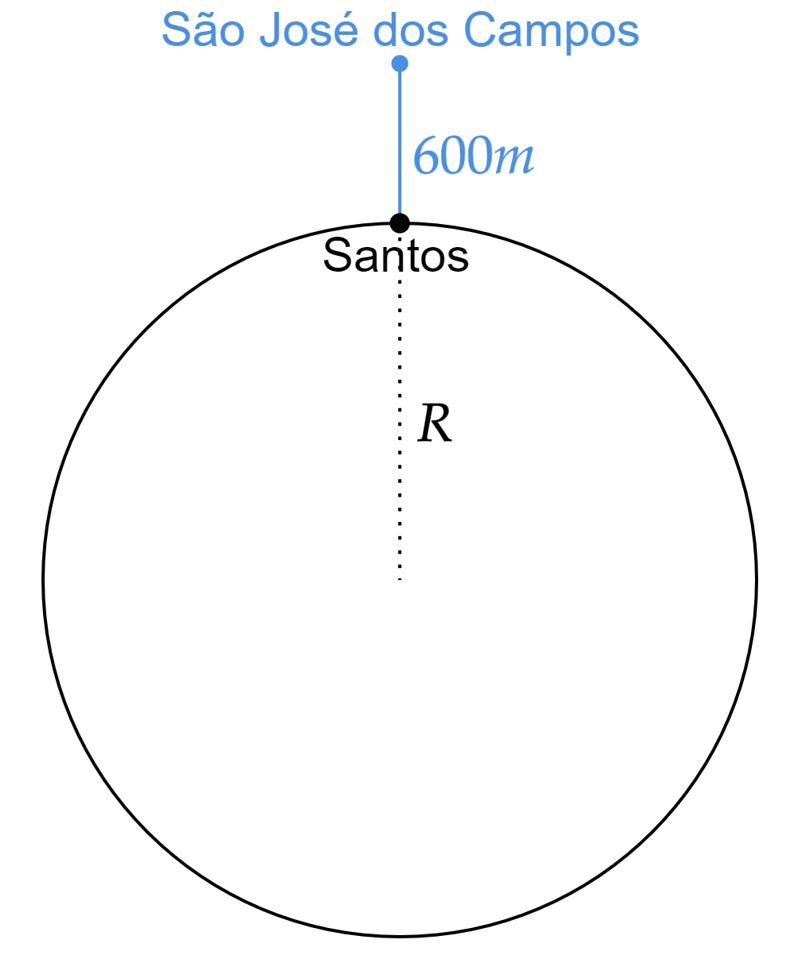Então a gravidade em cada caso é:\begin{matrix} \text{Santos}: & m \cdot g_1 = \dfrac{GMm}{(R)^2} &\Rightarrow& g_1 = \dfrac{GM}{(R)^2} \\ \text{São José dos Campos}: & m \cdot g_2 = \dfrac{GMm}{(R+600)^2} &\Rightarrow& g_2 = \dfrac{GM}{(R+600)^2} \end{matrix}Relacionando em $(1)$, temos:\begin{matrix} (T_1)^2 \cdot g_1 = (T_2)^2 \cdot g_2 &\Rightarrow& (T_1)^2 \cdot \left( \dfrac{1}{R^2} \right) = (T_1)^2 \cdot \left[ \dfrac{1}{(R+600)^2} \right] \end{matrix}Continuando,\begin{matrix} T_2 = T_1 \cdot \left(1 + \dfrac{600}{R} \right) \end{matrix}Com isso, nota-se que para cada segundo (período do pêndulo), o relógio atrasa um fator $600/R$. Conhecemos o raio da Terra, já foi dado, e este vale $6370 \ \pu{km}$. Além disso, repare nas alternativas, todas constam o atraso em dias, então:\begin{matrix} T_{atraso} = \dfrac{600}{6370 \cdot 10^3} \ \text{por segundo} \end{matrix}Sabido que um dia tem $86400 \ \pu{s}$, têm-se: \begin{matrix} 86400\cdot T_{atraso} = T_{atraso/dia} = \dfrac{600}{6370 \cdot 10^3} \cdot 86400 \approx 8 \ \text{segundos por dia} \end{matrix}\begin{matrix}Letra \ (B) \end{matrix}