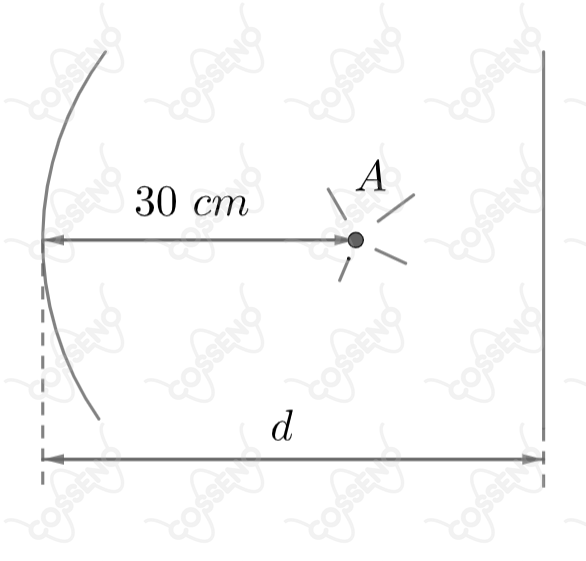
Um espelho plano está colocado em frente de um espelho côncavo, perpendicularmente ao eixo principal. Uma fonte luminosa , centrada no eixo principal entre os dois espelhos, emite raios que se refletem sucessivamente sobre os dois espelhos e formam sobre a própria fonte , uma imagem real da mesma. O raio de curvatura do espelho é e a distância do centro da fonte até o centro do espelho esférico é de . A distância do espelho plano até o centro do espelho côncavo é, então:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A priori, iremos definir o eixo à direita das abcissas como positivo, isto é, o foco positivo e, o vértice do espelho no centro $(0,0)$ do plano. Além disso, comecemos encontrando a posição da imagem conjugada do espelho côncavo, a qual servirá de objeto para o espelho plano. Dessa forma, segundo enunciado, temos:
\begin{matrix} {\dfrac{1}{f} = \dfrac{1}{x_o} + \dfrac{1}{x_i} } &\Rightarrow& {\dfrac{1}{20} = \dfrac{1}{30} + \dfrac{1}{x_i} } &\Rightarrow& \fbox{$x_i = 60 \ \pu{cm}$}
\end{matrix}Podemos pensar na situação como: \begin{matrix}
\text{(E. Côncavo)} &\underbrace{----}_{30 \ cm}& \text{(A)} &\underbrace{----}_{d - 30}& \text{(E. Plano)} &\underbrace{----}_{60-d}& (x_i)
\end{matrix}Logo, sabemos que $x_i$ atuará como objeto em relação ao espelho plano, e segundo enunciado, a imagem deve se formar sobre a fonte, o que implica:\begin{matrix} d - 30 = 60 - d &\Rightarrow& \fbox{$d = 45 \ \pu{cm}$}
\end{matrix} \begin{matrix} Letra \ (D)
\end{matrix}

