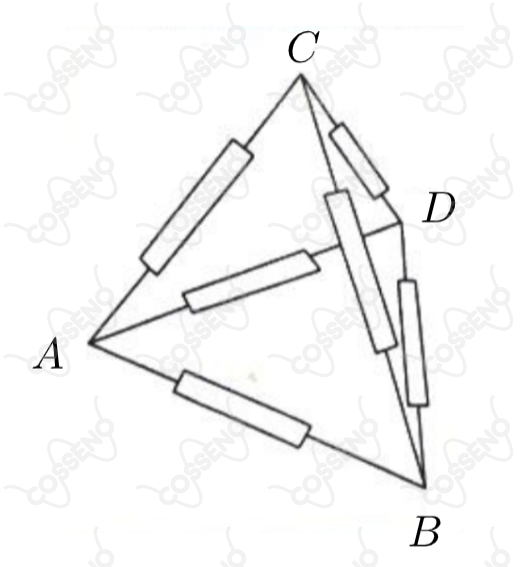
Considere um arranjo em forma de tetraedro construído com resistências de , como mostrado na figura. Pode-se afirmar que as resistências equivalentes e entre os vértices , , e , respectivamente, são:
Redesenhando o circuito:
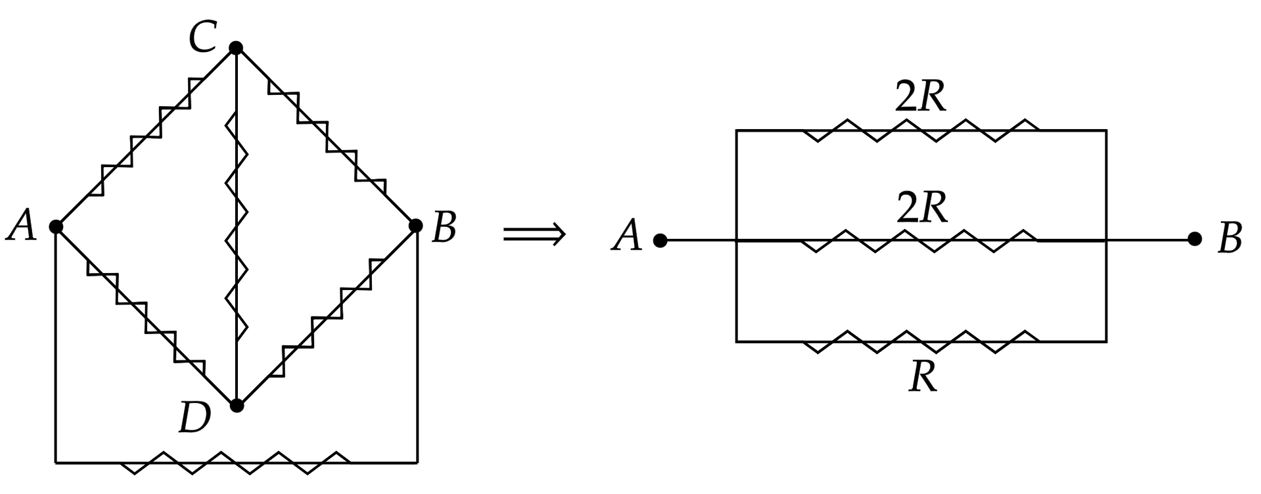Não é difícil perceber a simetria de um circuito losango, ou $\text{Ponte de Wheatstone}$, assim, resulta-se no circuito acima. Dessa forma, basta fazer uma associação em paralelo, veja: \begin{matrix} {{\dfrac{1}{R_{AB}}} = {{\dfrac{1}{2R}}}} + {{\dfrac{1}{R}}} + {{\dfrac{1}{2R}}} &\Rightarrow& R_{AB} = {\dfrac{R}{2}} &\therefore& \fbox{$R_{AB} = 50 \ \Omega$}
\end{matrix}Analogamente, a resistência $R_{CB}$ é idêntica, pois o processo é o mesmo, isto é, a simetria. Concluí-se então:
\begin{matrix} \fbox{$R_{AB} = R_{CD} = 50 \ \Omega$} \\ \\ Letra \ (B)
\end{matrix}
Ampliar Imagem
