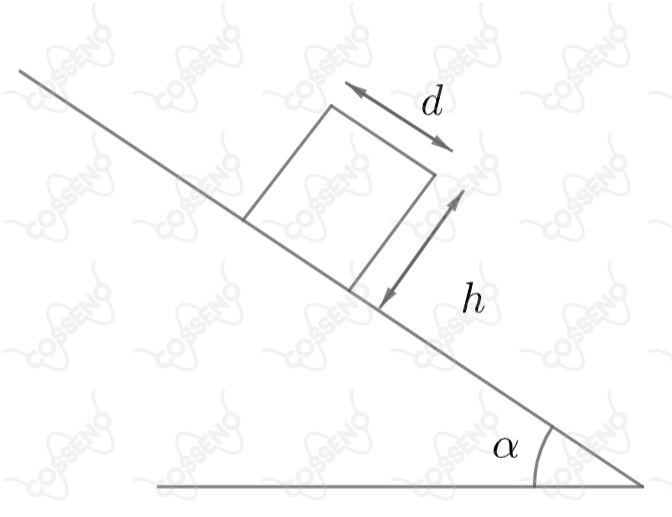
Considere um bloco de base e altura em repouso sobre um plano inclinado de ângulo . Suponha que o coeficiente de atrito estático seja suficientemente grande para que o bloco não deslize pelo plano. O valor máximo da altura para que a base permaneça em contato com o plano é:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Pensando na situação descrita, pode-se esboçar:
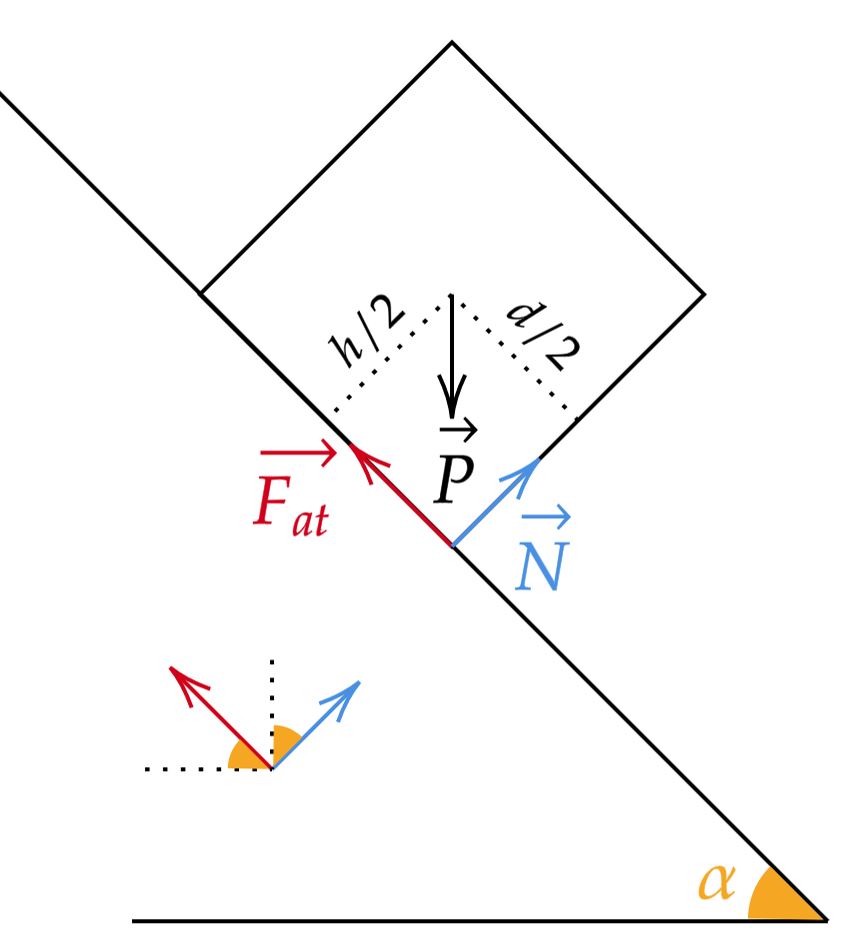 Atente que, na iminência de perder o contato toda reação da superfície será num ponto como mostra a imagem, esta é a iminência do tombamento. Nesse contexto, podemos analisar o momento das forças que atuam no corpo sobre o centro de gravidade, tal que:\begin{matrix} \Delta \vec{\tau} = 0 &\Rightarrow& F_{at} \cdot \left( \dfrac{h}{2} \right) = N \cdot \left( \dfrac{d}{2} \right) &\therefore& h = \dfrac{N}{F_{at}} \cdot d
\end{matrix}Analisando as forças $\vec{F}_{at}$ e $\vec{N}$, têm-se:\begin{matrix} \tan{\alpha} = \dfrac{F_{at}}{N} &\Rightarrow& \cot{\alpha} = \dfrac{N}{F_{at}} &\therefore& h = d \cdot \cot{\alpha} &\tiny{\blacksquare}&
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}
Atente que, na iminência de perder o contato toda reação da superfície será num ponto como mostra a imagem, esta é a iminência do tombamento. Nesse contexto, podemos analisar o momento das forças que atuam no corpo sobre o centro de gravidade, tal que:\begin{matrix} \Delta \vec{\tau} = 0 &\Rightarrow& F_{at} \cdot \left( \dfrac{h}{2} \right) = N \cdot \left( \dfrac{d}{2} \right) &\therefore& h = \dfrac{N}{F_{at}} \cdot d
\end{matrix}Analisando as forças $\vec{F}_{at}$ e $\vec{N}$, têm-se:\begin{matrix} \tan{\alpha} = \dfrac{F_{at}}{N} &\Rightarrow& \cot{\alpha} = \dfrac{N}{F_{at}} &\therefore& h = d \cdot \cot{\alpha} &\tiny{\blacksquare}&
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}

Ampliar Imagem
Seja $P$ o peso do bloco.
Note que a componente $P \cos \alpha$ de $P$ gera um torque $\tau_{1}$ no sentido anti-horário e a componente $P \sin\alpha$ de $P$ gera um torque $\tau_{2}$ no sentido horário , para o bloco não tombar devemos ter a seguinte condição $\tau_{1} \geq \tau_{2}$.
$\therefore$
$\tau_{1} \geq \tau_{2}$
$P \cos\alpha \cdot \dfrac{d}{2} \geq P \sin\alpha \cdot \dfrac{h}{2} $
$\implies h \leq d \cdot \cotg \alpha$
Portanto , o valor máximo de $h$ desejado é igual a $h_{max} = d \cdot \cotg \alpha$
$\text{Resposta : Alternativa D}$


