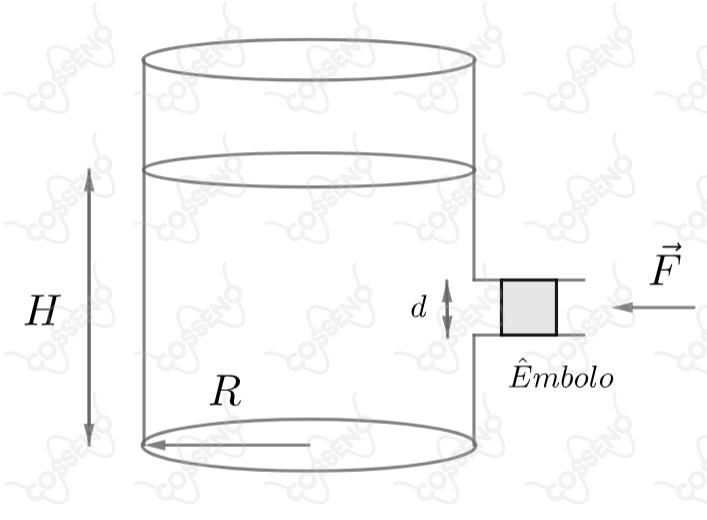
Um recipiente de raio e eixo vertical contém álcool até uma altura . Ele possui, à meia altura da coluna de álcool, um tubo de eixo horizontal cujo diâmetro é pequeno comparado a altura da coluna de álcool, como mostra a figura. O tubo é vedado por um êmbolo que impede a saída de álcool, mas que pode deslizar sem atrito através do tubo. Sendo a massa específica do álcool, a magnitude da força necessária para manter o êmbolo sua posição é:
Conhecido o conceito de pressão, temos que:\begin{matrix} P = \dfrac{F}{A} &\Rightarrow& F = P \cdot A &|& A = \pi \cdot \left(\dfrac{d}{2}\right)^2
\end{matrix}Observe que a pressão exercida sobre o êmbolo é devida a pressão interna da coluna de álcool, em que segundo enunciado, o tubo está à meia altura da coluna $H$. Nesse contexto, aplicando a $\text{Lei de Stevin}$:\begin{matrix} P - P_{atm} = \rho \cdot g \cdot \dfrac{H}{2} &\Rightarrow&
F_T = \left( \rho \cdot g \cdot \dfrac{H}{2} + P_{atm} \right) \cdot \pi \cdot \left(\dfrac{d}{2}\right)^2
\end{matrix}Continuando,\begin{matrix} F = F_T - F_{atm} &,& F_T = \underbrace{\dfrac{\rho g H \pi d^2}{8}}_{F} + \underbrace{\dfrac{P_{atm} \cdot \pi d^2}{4}}_{F_{atm}}
\end{matrix}Repare que $F_T$ é toda a força posta sobre o êmbolo, enquanto externamente temos a força $F$ mais a força atmosférica, esta que contribui com a força $F$. \begin{matrix}Letra \ (E)
\end{matrix}
