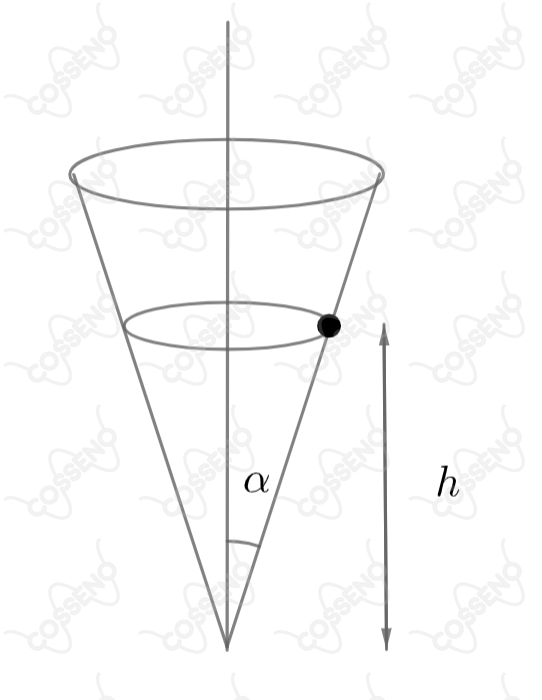
Uma massa puntual se move, sob a influência da gravidade e sem atrito, com velocidade angular em um circulo a uma altura na superfície interna de um cone que forma um ângulo com seu eixo central, como mostrado na figura. A altura da massa em relação ao vértice do cone é:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

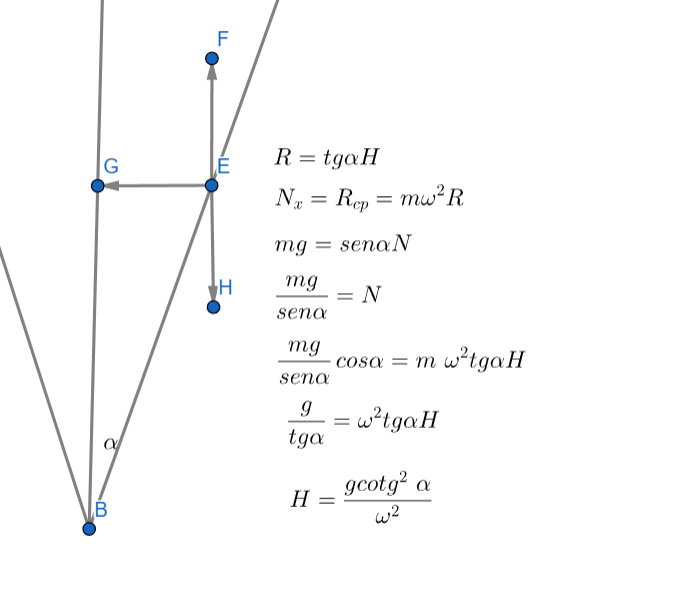
Pela geometria do problema, podemos tirar que: \begin{matrix} \tan{\alpha} ={{\dfrac{R}{h}}} &,& R = h\cdot \tan{\alpha} \end{matrix}Ao analisar os vetores que compõem o objeto, e por conseguinte decompor a normal, podemos escrever:\begin{matrix} \begin{cases} N\cdot \sin{\alpha} = m\cdot g \\ N\cdot \cos{\alpha} = F_{cp} \end{cases} &\Rightarrow&\tan{\alpha} = {{\dfrac{g}{a_{cp}}}} &\Rightarrow& \tan{\alpha}\cdot w^2\cdot R = g &\Rightarrow& \tan{\alpha}\cdot w^2\cdot h\cdot \tan{\alpha} = g &\therefore &\fbox{$h = {{\dfrac{g\cdot \cot^2{\alpha}}{w^2}}}$}
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}
Ampliar Imagem


