A priori, vamos analisar o movimento dos corpos, inicialmente, puxamos o forro para direita, nesse ato, o vaso tende a coibir este movimento, para isso, o atrito empurra o forro para esquerda. Por outro lado, com conhecimento da $\text{primeira lei de Newton}$, sabemos que se o vaso puxa o forro para esquerda, o forro puxa o vaso para direita. Desse modo, temos que ambos os corpos tendem a se mover para direita, digamos que o vaso apresente uma aceleração $b$, esta que pode ser encontrada a partir da análise de forças que atuam no bloco, veja: 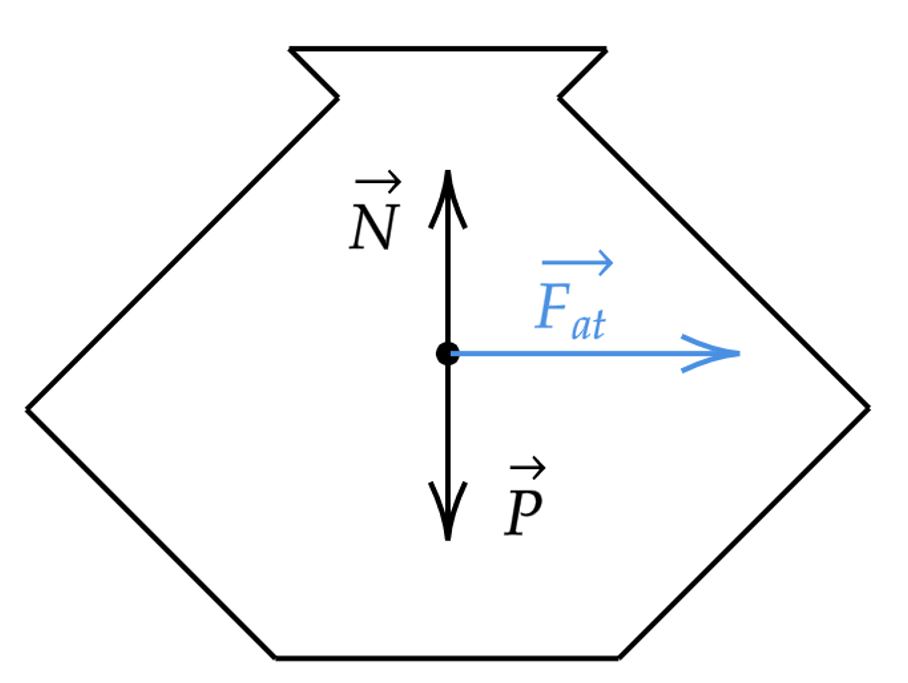Com isso, denotemos a massa do vaso de $m$, em que:\begin{matrix}\begin{cases}P &=&N \\ m \cdot b &=& F_{at} \end{cases}&\Rightarrow& b \le \mu \cdot g \end{matrix}Atente para o caso de maior estresse da força de atrito, neste tem-se a maior aceleração: $b=\mu \cdot g$, consequentemente, é o caso limite para análise. Neste viés, vamos assumir que tudo ocorra num tempo $t$, em que o vaso percorre uma distância $x$, logo:\begin{matrix} \Delta x = 0 \cdot t + b \cdot \dfrac{t^2}{2} &\Rightarrow&x = b \cdot \dfrac{t^2}{2} & (1) \end{matrix}Ao passo que o vaso deve cair sobre a mesa, entende-se que este percurso $x$ precisa ser menor que $D-d$, veja a imagem abaixo: 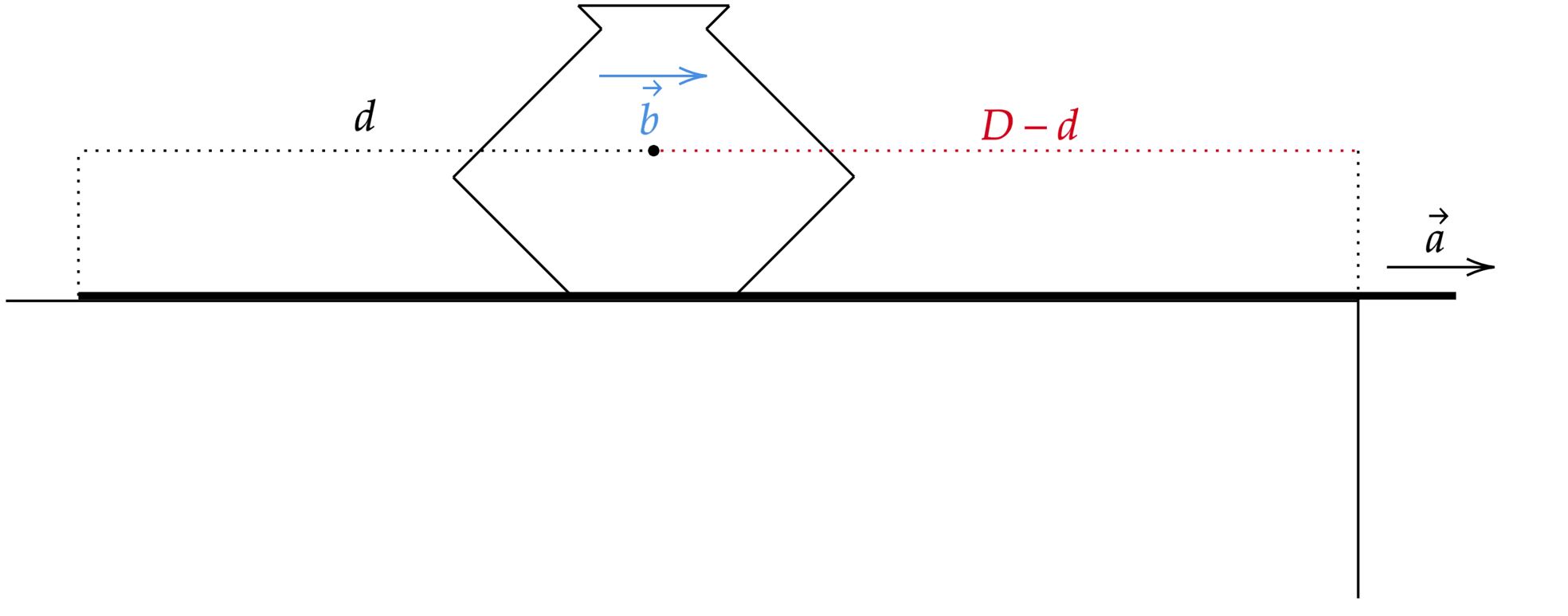Ora, sabendo que o caso limite é quanto o vaso cai sobre o extremo da mesa, deve-se ter que o extremo esquerdo do forro chegue antes, ou seja, o forro deve percorrer $D$ no tempo $t$, em que podemos equacionar:\begin{matrix} D = 0 \cdot t + a \cdot \dfrac{t^2}{2} &\Rightarrow&D = a \cdot \dfrac{t^2}{2} &\therefore& \dfrac{t^2}{2} = \dfrac{D}{a} \end{matrix}Substituindo o nosso resultado acima em $(1)$:\begin{matrix}x = b \cdot \dfrac{D}{a} \le D-d &\therefore& a \ge \dfrac{D}{D-d} \cdot \mu g \end{matrix}\begin{matrix}Letra \ (E) \end{matrix}