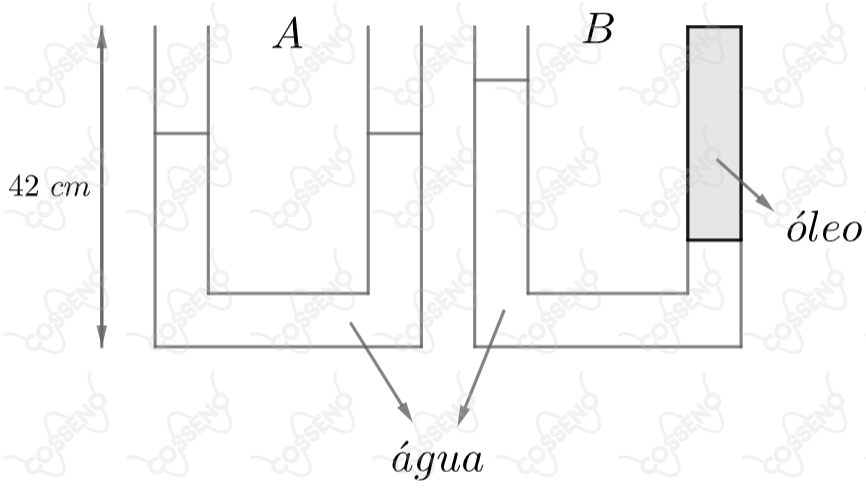
Um vaso comunicante em forma de possui duas colunas da mesma altura , preenchidas com água até a metade. Em seguida, adiciona-se óleo de massa específica igual a a uma das colunas até a coluna estar totalmente preenchida, conforme a figura . A coluna de óleo terá comprimento de:
CossenoGPT
Teste gratuitamente agora mesmo! 

Veja que os tubos são idênticos, assim, podemos dizer que o deslocamento da água de um lado é o mesmo do outro. Dessa forma, sabido a situação inicial em que a água está preenchida até metade do tubo, vamos inferir que ela varia $x$, enquanto a coluna de óleo preenche $y$.
$=> \ \ \ \ \ \ \ \text{Tubo esquerdo} \ \ \ \ \ :$ $(21+x)$
$=> \ \ \ \text{Tubo direito (óleo)} \ \ :$ $ \ \ \ (y)$
$=> \ \ \ \text{Tubo direito (água)} \ :$ $(21-x)$
Pelo $\text{Teorema de Stevin}$, traçando uma linha de nível no ponto de separação da água com o óleo, podemos escrever: \begin{matrix} P_1 = P_2 \\ \\ P_{atm} + \rho\cdot g\cdot (y) = P_{atm} + \mu\cdot g\cdot [(21+x)-(21-x)] \\ \\
\fbox{$\rho\cdot (y) = \mu\cdot (2x)$} \\ \color{gray}{\fbox{$\rho$: Densidade do óleo , $\mu$: Densidade da água}} \\ \\
\end{matrix} $\color{orangered}{Obs:}$ $\rho = 0,8 \dfrac{g}{\pu{cm^3}} \ \ \ , \ \ \ \mu = 1,0 \dfrac{g}{\pu{cm^3}}$
Novamente, pelo Teorema de Stevin, traçando uma linha de nível no ponto máximo da coluna de água da esquerda, podemos escrever: \begin{matrix} P_3 = P_{atm} \\ \\ P_{atm} + \rho\cdot g\cdot [y-(21+x)] = P_{atm} \\ \\
\fbox{$y =(21 + x)$} \\
\end{matrix}Resolvendo esse pequeno sistema: \begin{matrix} \begin{cases} 0,8y &=& 2x \\ y &=& (21 + x) \end{cases}
&\Rightarrow& \fbox{$y = 35 \ \pu{cm}$}
\end{matrix}\begin{matrix} Letra \ (D)
\end{matrix}
Denote $\rho_{água}$ como sendo a densidade da água , $\rho_{óleo}$ sendo a densidade do óleo $P_{atm}$ a pressão atmosférica e $g$ a gravidade atuante.
Seja $x$ o deslocamento da água do tubo , analisando os fluídos após ser adicionado óleo podemos constatar os seguintes fatos :
$\textbf{-}$ A altura da água do lado esquerdo do tubo é igual a $21 + x$
$\textbf{-}$ O comprimento do óleo é dado por $21 + x$
$\textbf{-}$ O altura da água do lado direito do tubo é igual a $21 -x$
Pelo Teorema de Stevin podemos escrever dessa forma que a pressão $P_{1}$ em um ponto do fundo do recipiente do lado esquedo do tubo e a pressão $P_{2}$ em um ponto do fundo do recipiente do lado direito do tubo é dado por
$\begin{cases}
P_{1} =P_{atm} + \rho_{água} \cdot (21 + x) \cdot g \\
P_{2} = P_{atm} + \rho_{óleo} \cdot (21 + x) \cdot g + \rho_{água} \cdot (21 - x) \cdot g
\end{cases}$
Como os pontos adotados tem o mesmo desnível , então
$P_{1} = P_{2}$
$P_{atm} + \rho_{água} \cdot (21 + x) \cdot g = P_{atm} + \rho_{óleo} \cdot (21 + x) \cdot g + \rho_{água} \cdot (21 - x) \cdot g$
$\implies \rho_{água} \cdot (21 + x) = \rho_{óleo} \cdot (21 + x) + \rho_{água} \cdot (21 - x) $
Sabendo que $ \rho_{água} = 1 \text{ g}/\text{cm}^3$ e que $ \rho_{óleo} = 0,8 \text{ g}/\text{cm}^3$ temos que
$1 \cdot (21 + x) = 0,8 \cdot (21 + x) + 1 \cdot (21-x) $
$0,2\cdot (21+x) = 21 - x$
$\implies 2 \cdot (21+x) = 10\cdot (21 - x)$
$42 +2x = 210 - 10x \implies 12x = 168 \implies x = 14 \text{ cm}$
Portanto , o comprimento de óleo é dado por $\boxed{21 + x = 35 \text{ cm}}$
$\textbf{Resposta : Alternativa D}$


