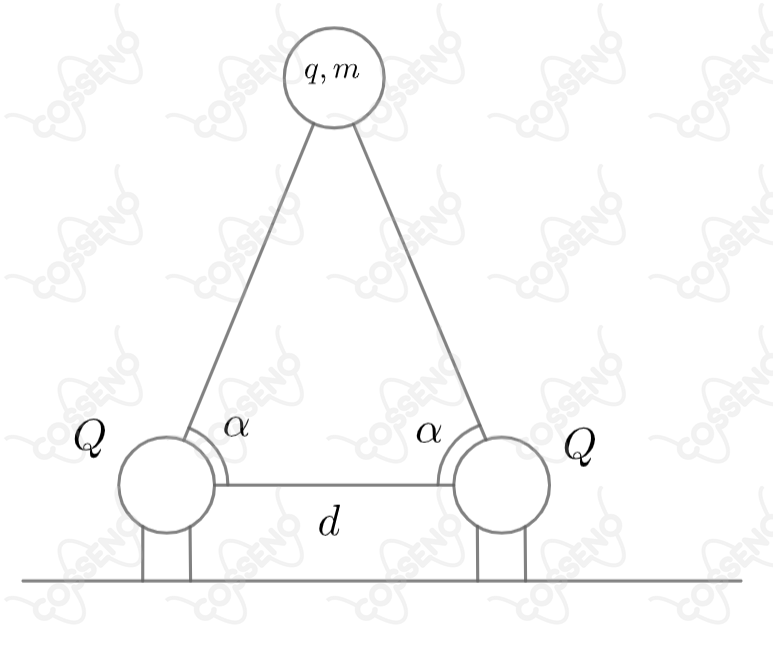
Uma pequena esfera de massa e carga , sob a influência da gravidade e da interação eletrostática, encontra-se suspensas por duas cargas fixas, colocadas a uma distância no plano horizontal, como mostrado na figura. Considere que a esfera e as duas cargas fixas estejam no mesmo plano vertical, e que sejam iguais a os respectivos ângulos entre a horizontal e cada reta passando pelos centros das cargas fixas e da esfera. A massa da esfera é então:
Da situação do enunciado, temos:
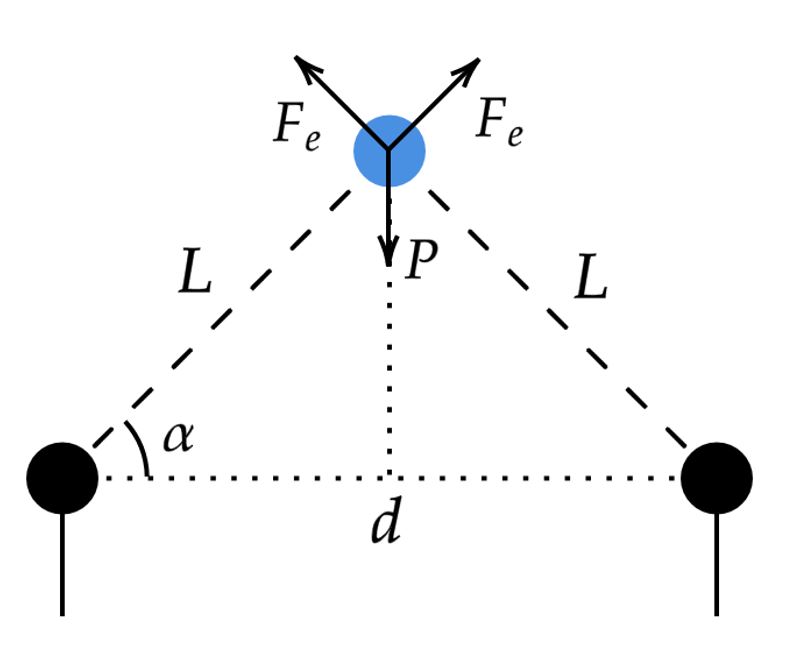Veja que, ao decompor as forças elétricas, encontramos: \begin{matrix} P = 2F_e\sin{\alpha} &\Rightarrow& mg = 2 \cdot {\left( \dfrac{KQq\sin{\alpha}}{L^2} \right)} &\Rightarrow& m = 2 \cdot {\left( \dfrac{Qq\sin{\alpha}}{4\pi\epsilon_ogL^2} \right)} &\color{royalblue}{,}& \color{royalblue}{K = {\dfrac{1}{4\pi\epsilon_0}}}
\end{matrix} Agora, da trigonometria do problema, temos: \begin{matrix} L = {\dfrac{d}{2\cos{\alpha} } } &\Rightarrow& \fbox{$m = 8\cdot {\left(\dfrac{Qq\cos^2{\alpha}\sin{\alpha}}{4\pi\epsilon_ogd^2}\right)}$}
\end{matrix} \begin{matrix} Letra \ (D)
\end{matrix}
Ampliar Imagem
