A priori, o enunciado não deixa explícito se podemos ou não desprezar o peso dos pratos, assim como da barra desnivelada na balança, todavia, ele o faz pois o resultado é mesmo em ambos os casos. Veja que, podemos denotar a massa da barra de $M$, em que a situação descrita pode ser representada como: 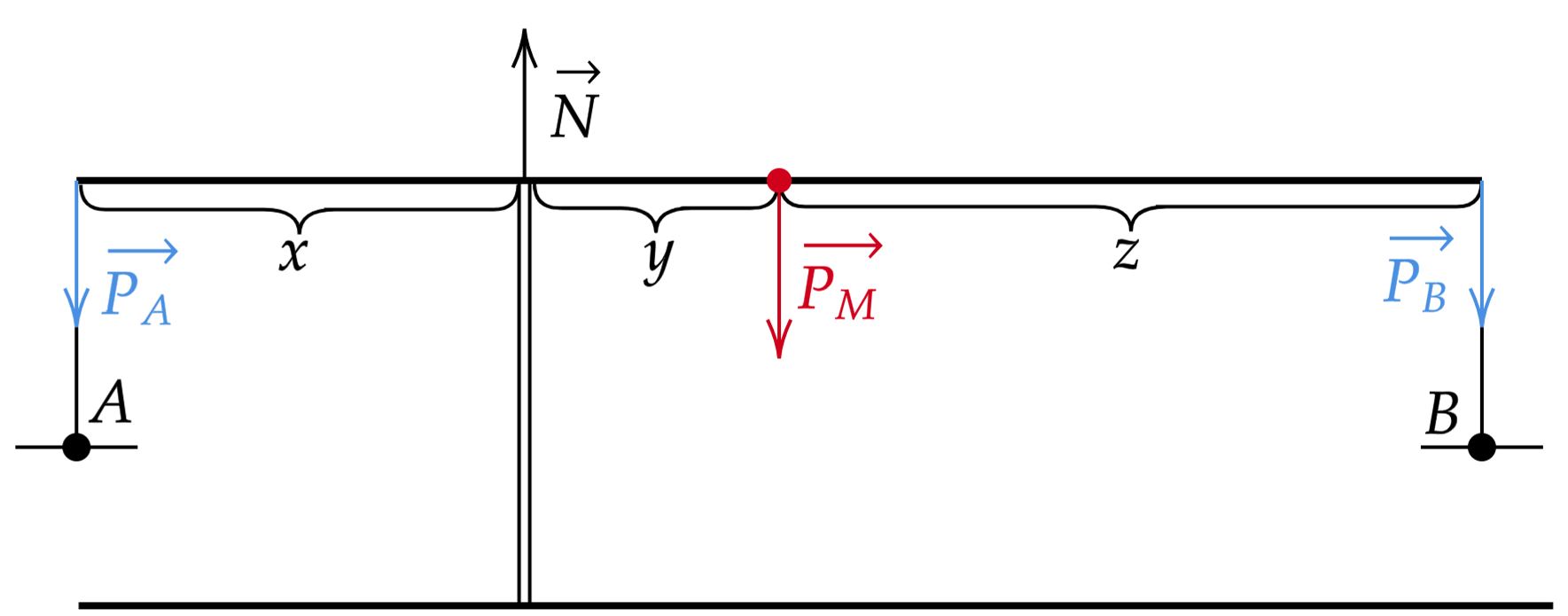Analisando o momento das forças na barra em relação ao ponto de contato que a sustenta, temos:\begin{matrix} P_A \cdot x = P_M \cdot y + P_B \cdot (y+z) &\Rightarrow& (m_A + ?_A )\cdot x = M \cdot y + (m_B + ?_B)\cdot (y+z) \end{matrix}Repare que "$?$" expressa a massa a qual iremos colocar, analisando a expressão, não é difícil inferir que:\begin{matrix}?_A \cdot x = \ ?_B \cdot (y+z) \end{matrix}Então para cada caso, têm-se: \begin{matrix}\begin{cases} m \cdot x &=& p \cdot (y+z) \\ q \cdot x &=& m \cdot (y+z) \end{cases} &\Rightarrow& \dfrac{m}{q} = \dfrac{p}{m} &\therefore& m = \sqrt{p\cdot q} \end{matrix}$\color{orangered}{\text{Obs:}}$ Pela primeira expressão que encontramos, é visível que, se as massas da polia e dos pratos fossem desprezíveis, o resultado seria o mesmo.\begin{matrix}Letra \ (B) \end{matrix}