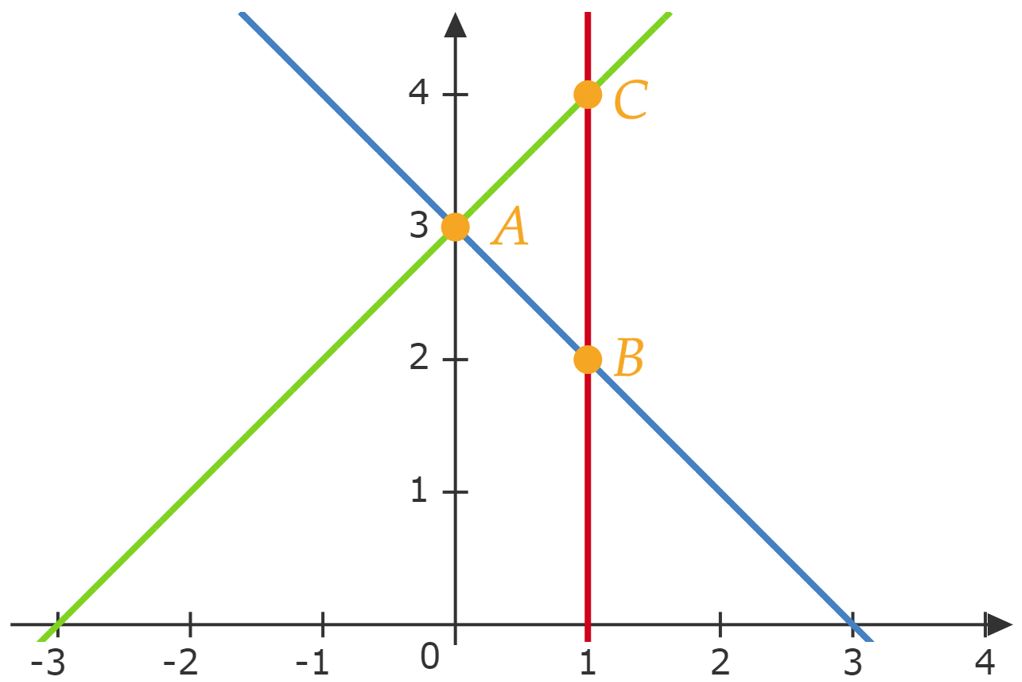
Seja o ponto de intersecção das retas e dadas, respectivamente pelas equações e . Sejam e pontos situados no primeiro quadrante com e . sabendo que , então a reta passando por e é dada pela equação:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A priori, veja que as retas são perpendiculares, pois, $m_r.m_s=-1$ , assim, encontrando o ponto $A$ a partir do sistema de equações formado pelas retas: \begin{matrix} \begin{cases} x+y &=& 3 \\ x-y&=& -3
\end{cases} &\therefore& x =0 &,& y = 3
\end{matrix}
Desse modo, com conhecimento do ponto $A:(0,3)$, aplicando a $\text{Distância Euclidiana}$ entre os pontos $A:(0,3)$ , $B:(a,b)$ e $C:(c,d)$ , temos:
\begin{matrix} d(A,B) = \sqrt{2} &\Rightarrow& (a-0)^2 + (b-3)^2 = 2 \\
d(A,C) = \sqrt{2} &\Rightarrow& (c-0)^2 + (d-3)^2 = 2
\end{matrix}Já segundo as equações das retas: \begin{matrix} \begin{cases} a+b &=& 3 \\ c-d&=& -3
\end{cases} &\Rightarrow& a^2 = (b-3)^2 &,& c^2 = (d-3)^2
\end{matrix} Substituindo nossos resultados, encontramos, \begin{matrix} a^2 = 1 &,& c^2 = 1
\end{matrix} Como o enunciado afirma os pontos estarem no primeiro quadrante, \begin{matrix} a = c = 1
\end{matrix} Substituindo nas equações das retas, \begin{matrix} b = 2 &,& d = 4
\end{matrix}Agora, conhecido os pontos $B:(1,2)$ e $C:(1,4)$, não é difícil encontrar a equação da reta, ela obrigatoriamente deve ser vertical, sendo ela $\fbox{$x = 1$}$
 \begin{matrix} Letra \ (D)
\end{matrix}
$\color{orangered}{Obs:}$ Você pode verificar esse resultado a partir da condição de alinhamento entre três pontos.
\begin{matrix} Letra \ (D)
\end{matrix}
$\color{orangered}{Obs:}$ Você pode verificar esse resultado a partir da condição de alinhamento entre três pontos.

Ampliar Imagem

