A princípio, podemos escrever:\begin{matrix} x = \arctan{\dfrac{1}{1+e^x}} &,& y = \arctan{\dfrac{1-e^{2x}}{1+e^x}} \end{matrix}$\color{orangered}{\text{Obs:}}$\begin{matrix} (1-e^x) \cdot \color{#3368b8}{\dfrac{(1+e^x)}{(1+e^x)}} = \dfrac{1-e^{2x}}{1+e^x} \end{matrix}Nesse contexto, vamos partir encontrando $x-y$, para isso, têm-se: \begin{matrix} \tan{(x-y)} = \dfrac{\tan{x} - \tan{y}}{1 + \tan{x} \tan{y}} = \dfrac{ \dfrac{1}{1+e^x} - \dfrac{1-e^{2x}}{1+e^x}}{1 + \dfrac{1}{1+e^x} \cdot \dfrac{1-e^{2x}}{1+e^x} } = \dfrac{e^{2x}}{2} \end{matrix}Então,\begin{matrix} (x - y) = \arctan{\dfrac{e^{2x}}{2}} \end{matrix}Com isso, podemos substituir nosso resultado acima na expressão do enunciado e encontrar:\begin{matrix} \sec{ \left[ \arctan{\dfrac{e^{2x}}{2}}\right]} = \dfrac{\sqrt{5}}{2} &\Rightarrow& \cos{ \left[ \arctan{\dfrac{e^{2x}}{2}}\right]} = \dfrac{2}{\sqrt{5}} \end{matrix}Pensando num triângulo retângulo, conseguimos esboçar: 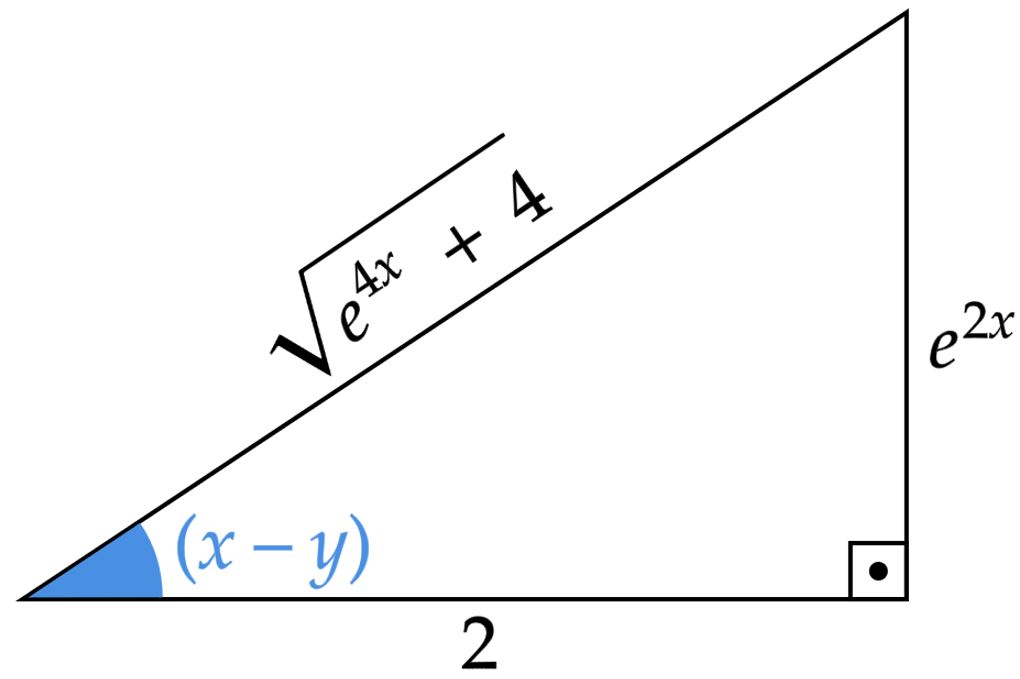Desse modo, nota-se que:\begin{matrix} \cos{(x-y)} = \dfrac{2}{\sqrt{e^{4x} +4}} = \dfrac{2}{\sqrt{5}} \end{matrix}Logo,\begin{matrix} \sqrt{e^{4x} +4} = \sqrt{5} &\Rightarrow& e^{4x} = 1 &\therefore& x = 0 & \tiny{\blacksquare} \end{matrix}Analisando as alternativas, a única que satisfaz o nosso resultado acima é a:\begin{matrix}Letra \ (D) \end{matrix}